Trier une liste de textes par calcul matriciel

Pour partager cette vidéo sur les réseaux sociaux ou sur un site, voici son url :


Sujets que vous pourriez aussi aimer :


Trier des listes de textes attachés

Nous avons déjà appris à trier des listes de textes indépendants par formules matricielles avec Excel.



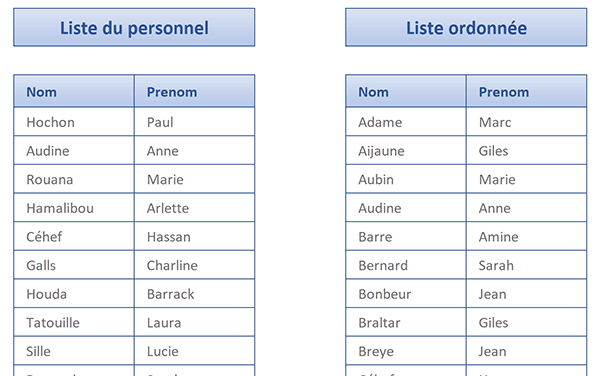
Mais lorsqu'il s'agit de faire suivre des données attachées, comme ici les prénoms d'une seconde colonne associée aux noms, la problématique se corse quelque peu. Et c'est cette organisation alphabétique conjointe que nous proposons de résoudre dans cette formation.

Source et présentation
Pour exercer ces travaux, nous suggérons tout d'abord de réceptionner un classeur offrant cette liste de données désorganisée.

• Télécharger le classeur trier-textes-par-calculs.xlsx en cliquant sur ce lien,
• Double cliquer sur le fichier téléchargé pour l'ouvrir dans Excel,
• Puis, cliquer sur le bouton Activer la modification du bandeau de sécurité,

Le tableau de gauche dresse la liste des salariés avec leurs noms et prénoms. Celui de droite, entre les colonnes E et F, est vide pour l'instant. Il doit recomposer cette même liste réorganisée par ordre alphabétique croissant, à l'aide d'une formule matricielle.

En déployant la zone Nom en haut à gauche de la feuille Excel, vous notez que des intitulés ont été attribués à certaines colonnes. Les deux premières matrices sont reconnues par leurs noms de champs, soit respectivement Nom et Prénom. La première matrice d'extraction, celle des noms triés en colonne E, est reconnue par l'intitulé nomsT.

Ces noms aideront à simplifier la syntaxe de la formule matricielle à bâtir. Et pour la bonne compréhension du processus et du raisonnement, nous proposons de décomposer les calculs en plusieurs étapes. Ensuite, nous les regrouperons dans une unique formule.

Ordre des textes
Pour déterminer l'ordre alphabétique des noms dans le tableau d'origine, nous allons réaliser un dénombrement conditionnel matriciel. Il s'agit donc d'exploiter la fonction Nb.Si. Le critère consiste à savoir quels sont les noms inférieurs aux autres. Ce procédé est peu habituel. Excel considère les premières lettres de l'alphabet comme les plus petites et les dernières comme les plus grandes. C'est ainsi que les comparaisons sont rendues possibles et que le dénombrement révèlera les positions à rétablir. Pour ces remarques, nous allons travailler dans des colonnes arbitraires.

• Sélectionner par exemple la plage de cellules H6:H63,
• Construire la formule matricielle suivante : =NB.SI(Nom;'<=' & Nom),
• Puis, valider nécessairement le calcul par le raccourci clavier CTRL + MAJ + Entrée,

Nous obtenons toute une série de valeurs numériques, mais pas n'importe lesquelles. Il s'agit des positions dans lesquelles devraient être rangés les enregistrements, dans le cas d'un tri croissant. Par exemple, le chiffre 4 est associé à la personne Audine Anne. Elle doit donc intervenir en quatrième position dans le tableau de la liste ordonnée. La raison est simple grâce au raisonnement matriciel enclenché avec la fonction Nb.Si. Sur la matrice des noms, nous cherchons à comptabiliser pour chacun, tous ceux qui sont considérés comme inférieurs ou égaux ('<=' & Nom). En d'autres termes, il s'agit de ceux qui sont situés avant dans l'ordre alphabétique, car considérés comme plus petits. 3 personnes devront donc être classées avant Audine Anne. La quatrième du dénombrement correspond à elle-même.

Matrice virtuelle d'analyse
Pour exploiter cette information de dénombrement renseignant sur les positions à adopter, nous devons réaliser une analyse sur la hauteur complète de la matrice des noms. C'est ainsi que la fonction Equiv pourra ensuite renseigner sur la position d'origine des enregistrements concernés à réorganiser les uns à la suite des autres.

• Sélectionner la plage de cellules I6:I63,
• Construire la formule matricielle suivante : =LIGNE(INDIRECT('1:' & LIGNES(Nom))),
• Puis, valider nécessairement le calcul par le raccourci clavier CTRL + MAJ + Entrée,

Nous obtenons des nombres incrémentés sur la hauteur totale de la matrice. Ces numéros représentent chaque enregistrement. C'est ainsi que nous allons pouvoir les repérer en les confrontant aux positions révélées par le calcul de dénombrement. Dans sa version standard, la fonction Ligne retourne l'indice de ligne d'une cellule qui lui est passée en paramètre. Ici, nous lui transmettons une matrice de même hauteur que la source de données. Pour cela, nous la faisons débuter à partir de la première ligne ('1:'). Puis, nous l'étendons sur la hauteur de la colonne grâce à la fonction Lignes. Cette fonction est le pluriel de la précédente et ne retourne pas du tout la même information. Elle renseigne sur la hauteur d'un tableau. Ici, nous lui transmettons la matrice des noms. Il en résulte le décompte de cette rangée, conduisant à ces nombres incrémentés du fait du raisonnement matriciel.

Trouver les positions d'origine
Désormais, nous devons déterminer les positions de chaque personne identifiée par son dénombrement, correspondant à sa nouvelle position à adopter. C'est bien sûr la fonction Equiv qui doit être employée, toujours dans un raisonnement matriciel. En guise de valeur cherchée, nous allons lui transmettre la matrice virtuelle précédemment construite. Et en guise de tableau de recherche, nous allons lui passer le dénombrement conditionnel réalisé lors du premier calcul. Ainsi, chaque nom sera étudié, repéré par son dénombrement et identifié en ligne.

• Sélectionner la plage de cellules J6:J63,
• Taper le symbole égal (=) pour initier la formule matricielle,
• Inscrire la fonction donnant les positions, suivie d'une parenthèse, soit : Equiv(,
• En guise de valeur cherchée, transmettre la matrice virtuelle précédemment construite :

LIGNE(INDIRECT('1:' & LIGNES(Nom)))

• Taper un point-virgule (;) pour passer dans le deuxième argument de la fonction Equiv,
• En guise de tableau de recherche, transmettre le dénombrement conditionnel précédent :

NB.SI(Nom;'<='& Nom)

• Taper un point-virgule suivi du chiffre zéro : ;0, pour réaliser une recherche exacte,
• Fermer la parenthèse de la fonction Equiv,
• Enfin, valider nécessairement la formule matricielle par le raccourci CTRL + MAJ + Entrée,

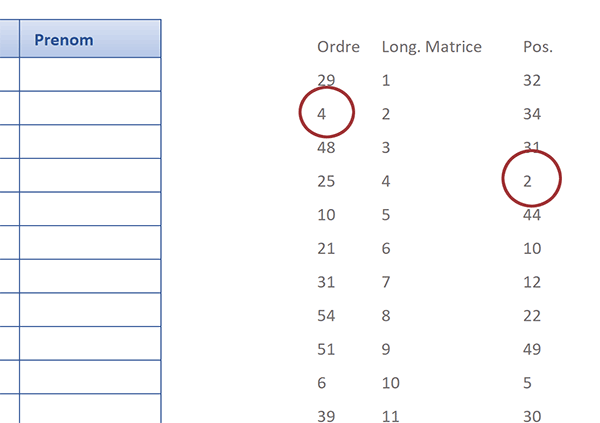
Les positions calculées tombent. Elles indiquent dans quel ordre les enregistrements doivent être réorganisés pour un tri croissant. Ainsi, ce sont les personnes placées en 32, 34 et 31^ème positions qui doivent désormais apparaître aux trois premières places. Et le quatrième résultat vient parfaitement corroborer le premier calcul de dénombrement. Il indique que Audine Anne, placée actuellement en deuxième position, doit être décalée en quatrième place.

Extraire les enregistrements triés
Il ne nous reste plus qu'à exploiter ces positions dévoilées pour réorganiser l'information. Pour cela, il s'agit d'extraire les données dans l'ordre indiqué par la fonction Equiv. Nous devons donc l'imbriquer dans la fonction d'extraction Index.

• Sélectionner la première cellule du précédent calcul, soit J6,
• Dans sa barre de formule, sélectionner l'intégralité de sa syntaxe sans le symbole égal,
• La copier par le raccourci clavier CTRL + C par exemple,
• Puis, sortir de la barre de formule par le raccourci CTRL + MAJ + Entrée,
• Sélectionner tous les noms à réorganiser, soit la plage de cellules E6:E63,
• Taper le symbole égal (=) pour initier la formule matricielle d'extraction,
• Inscrire la fonction d'extraction suivie d'une parenthèse, soit : Index(,
• Désigner la matrice des valeurs à extraire par son nom, soit : Nom,
• Taper un point-virgule (;) pour passer dans l'argument des indices de ligne,
• Coller le précédent calcul par le raccourci clavier CTRL + V par exemple,
• Puis, fermer la parenthèse de la fonction Index,
• Enfin, valider nécessairement la formule matricielle par le raccourci CTRL + MAJ + Entrée,

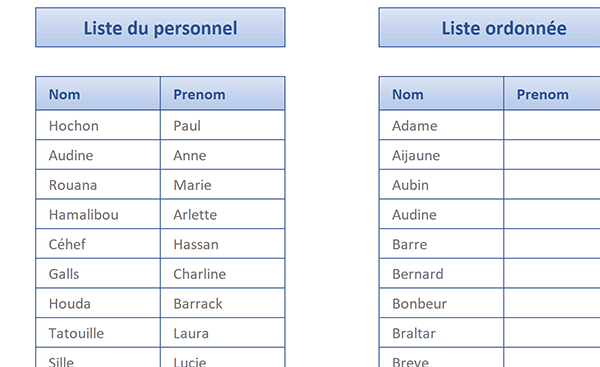
Comme vous pouvez le voir, tous les noms sont parfaitement réorganisés par ordre alphabétique croissant. Et pour cela, une seule formule matricielle a été nécessaire. La syntaxe complète de cette dernière est la suivante :

{=INDEX(Nom; EQUIV(LIGNE(INDIRECT('1:' & LIGNES(Nom))); NB.SI(Nom;'<='& Nom); 0))}

Extraire les prénoms attachés aux noms triés
L'enjeu consiste désormais à importer les prénoms attachés aux noms triés pour une réorganisation globale des informations. Pour cela, nous devons extraire les prénoms du tableau d'origine en décelant leurs positions selon la correspondance établie entre les noms triés et les noms d'origine. Cette correspondance doit se faire par la fonction Equiv imbriquée dans la fonction Index pour l'extraction.

• Sélectionner tous les prénoms à rapatrier, soit la plage de cellules F6:F63,
• Taper le symbole égal (=) pour initier la formule matricielle d'extraction,
• Inscrire la fonction d'extraction suivie d'une parenthèse, soit : Index(,
• Désigner les valeurs à extraire par le nom de la matrice, soit : Prenom,
• Taper un point-virgule (;) pour passer dans l'argument des positions à déceler,
• Inscrire la fonction cherchant ces positions, suivie d'une parenthèse, soit : Equiv(,
• Désigner les précédents extraits par l'intitulé de plage, soit : NomsT,
• Taper un point-virgule (;) pour passer dans l'argument du tableau de recherche,
• Désigner la matrice des noms d'origine, soit : Nom,
• Taper un point-virgule suivi du chiffre zéro : ;0, pour réaliser une recherche exacte,
• Fermer la parenthèse de la fonction Equiv,
• Puis, fermer la parenthèse de la fonction Index,

Comme précédemment, nous ne renseignons pas le troisième paramètre de la fonction Index. Il concerne la position en colonne de l'information à extraire. Celle-ci est implicitement connue. En effet, en premier paramètre de la fonction Index, nous avons transmis une matrice d'extraction constituée d'une seule colonne.

• Enfin, valider nécessairement la formule matricielle par le raccourci CTRL + MAJ + Entrée,

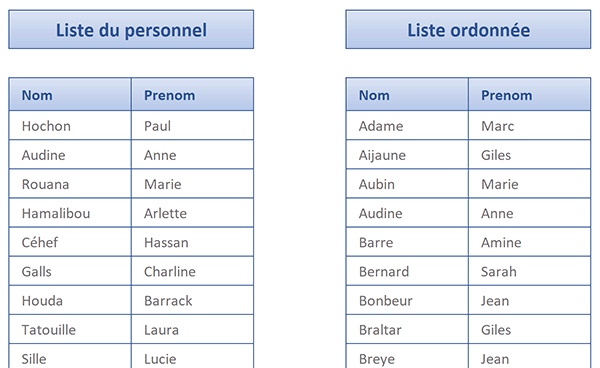
Comme vous pouvez le voir, tous les prénoms sont parfaitement importés, en respectant l'organisation ordonnée sur les noms triés. La formule matricielle que nous avons bâtie est la suivante :

=INDEX(Prenom; EQUIV(nomsT; Nom; 0))

Nous avons extrait les prénoms tout en recherchant les positions des concordances entre les noms extraits et triés (nomsT) et les noms de la liste d'origine (Nom).