Comparer deux listes de données avec Excel

Pour partager cette vidéo sur les réseaux sociaux ou sur un site, voici son url :


Sujets que vous pourriez aussi aimer :


Valeurs uniques et doublons

Grâce aux calculs matriciels, nous pouvons comparer assez facilement deux listes de données. Ici, nous proposons de les mettre à contribution pour extraire et isoler d'une part les valeurs uniques et d'autre part les données en double.



Dans l'exemple finalisé illustré par la capture ci-dessus, nous comparons deux listes nommées respectivement Champ A et Champ B. Elles énumèrent des villes. Dans la colonne Id. Uniques, nous parvenons à extraire les villes non concordantes entre les deux listes. Puis, nous les regroupons dans la première colonne nommée Extraire. De la même façon, nous isolons les redondances dans la colonne Id. Doublons. Puis, nous les regroupons dans sa colonne voisine. Ce sont bien sûr des formules matricielles qui permettent ces prouesses. Et nous proposons de les étudier.

Source de données
Pour réaliser ces travaux, nous proposons de récupérer ces listes à comparer.

• Télécharger le classeur extraire-uniques-et-doublons.xlsx en cliquant sur ce lien,
• Double cliquer sur le fichier téléchargé pour l'ouvrir dans Excel,
• Puis, cliquer sur le bouton Activer la modification du bandeau de sécurité,

Nous réceptionnons une feuille sur laquelle les deux listes à comparer sont effectivement remplies de villes parfois communes et parfois différentes. Les quatre colonnes suivantes sont fort naturellement vides à ce stade. Elles attendent les formules matricielles d'extraction.

En déployant la zone Nom, en haut à gauche de la feuille Excel, vous notez que quatre colonnes sont identifiées par des intitulés. Il s'agit premièrement des deux listes à comparer. Mais il s'agit aussi des deux premières colonnes respectives d'extraction.



Nous exploiterons ces noms pour simplifier la construction et la compréhension des formules matricielles.

Isoler les valeurs uniques
Dans la formation précédente, grâce à la fonction Equiv, nous avions avancé une solution pour repérer les données identiques. Mais cette fonction ne dévoile ces positions que lorsque la concordance est avérée. Dans le cas des données uniques, elle ne peut identifier les dissonances entre deux listes. C'est tout l'intérêt de ces travaux. Dans le cadre d'un raisonnement matriciel, la fonction Excel Nb.Si est capable de déterminer chaque enregistrement non trouvé dans une autre liste. Et c'est ce que nous allons démontrer.

• Sélectionner toutes les cellules de la colonne Id. Uniques, soit la plage F4:F14,
• Taper le symbole égal (=) pour débuter la formule matricielle,
• Saisir la fonction conditionnelle suivie d'une parenthèse, soit : Si(,

En effet, nous devons vérifier si le décompte de chaque ville produit un résultat d'une liste à une autre. Un critère est donc nécessaire.

• Inscrire la fonction de dénombrement conditionnel suivie d'une parenthèse, soit : Nb.Si(,
• Désigner la première liste à comparer par son nom, soit : champa,
• Taper un point-virgule (;) pour passer dans l'argument du critère à dénombrer,
• Désigner la seconde liste à comparer par son nom, soit : champb,
• Fermer la parenthèse de la fonction Nb.Si,
• Puis, taper l'égalité suivante : =0,

En guise de critère, nous passons à la fonction Nb.Si l'intégralité des données de la colonne champb. Dans un processus matriciel, ce sont donc toutes les valeurs de la première liste (champa) qui seront comparées avec celles de la seconde liste (champb). Avec cette égalité, nous cherchons à identifier toutes les données qui ne sont pas trouvées d'une liste à une autre. Si cette condition est remplie, nous savons que la ville n'existe pas en double. De fait, elle doit être extraite.

• Taper un point-virgule (;) pour passer dans la branche Alors de la fonction Si,
• Désigner la deuxième liste par son nom, soit : champb,

Ainsi, lorsque la condition matricielle est satisfaite, la ville de l'enregistrement concordant, donc unique, issue de la seconde liste, doit être inscrite et restituée. Dans le cas contraire en revanche, nous devons conserver vide la cellule du résultat.

• Taper un point-virgule (;) pour passer dans la branche Sinon de la fonction Si,
• Inscrire deux guillemets ('') pour garder la cellule vide en cas de doublon,
• Fermer la parenthèse de la fonction Si,
• Enfin, valider nécessairement la formule matricielle par le raccourci CTRL + MAJ + Entrée,

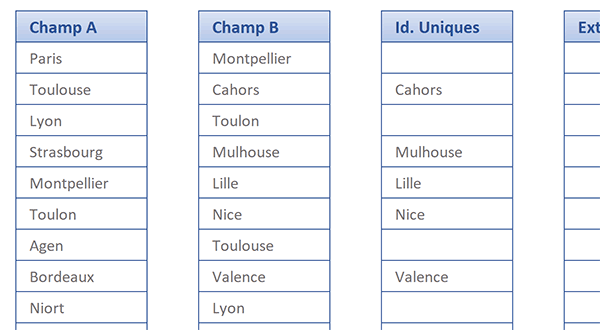
Les deux listes à comparer sont relativement courtes. En les étudiant rapidement, vous notez que seules les données divergentes ont en effet été extraites et isolées selon le calcul matriciel suivant :

{=SI(NB.SI(champa;champb)=0; champb; '')}

Néanmoins, elles ne sont pas encore regroupées. Des espaces vides les séparent. C'est l'objectif du calcul suivant. Mais avant cela, nous proposons d'isoler les données redondantes dans la colonne Id. Doublons. L'adaptation de la formule matricielle est effectivement triviale. Il suffit de remplacer l'égalité du dénombrement par une inégalité.

• Sélectionner toutes les cellules de la rangée Id. Doublons, soit la plage J4:J14,
• Adapter la formule matricielle précédente comme suit :

{=SI(NB.SI(champa;champb)>0; champb; '')}

Grâce à l'inégalité du dénombrement, nous cherchons à restituer toutes les valeurs recensées dans la première liste et dans la seconde, soit les doublons. A validation, ce sont en effet les redondances qui apparaissent. D'ailleurs, elles sont précisément positionnées sur les lignes vides de la précédente extraction.

Regrouper les données extraites
Pour regrouper les informations extraites, nous devons utiliser la fonction Excel Grande.Valeur, bien évidemment dans un raisonnement matriciel. Pour cela, nous devons identifier toutes les positions des données isolées, bien sûr grâce à la fonction Equiv. En guise de rang, nous fournirons à la fonction Grande.Valeur, une matrice virtuelle de la même hauteur que celle des listes comparées. Ainsi, nous extrairons tous les rangs potentiels concordants avec les positions calculées pour restituer les données regroupées.

• Sélectionner toutes les cellules de la première colonne Extraire, soit la plage H4:H14,
• Taper le symbole égal (=) pour initier la formule matricielle,
• Inscrire la fonction de gestion des anomalies suivie d'une parenthèse, soit : SiErreur(,

En effet, les fonctions d'extraction retournent des erreurs lorsque les valeurs cherchées ne sont pas trouvées. Et dans la liste à regrouper, on dénombre des cellules vides.

• Inscrire la fonction d'extraction suivie d'une parenthèse, soit : Index(,
• Désigner la colonne précédente par son nom comme matrice de recherche, soit : idu,
• Taper un point-virgule (;) pour passer dans l'argument des positions en ligne,
• Inscrire la fonction des grandes valeurs suivie d'une parenthèse, soit : Grande.Valeur(,
• Taper la fonction conditionnelle suivie d'une parenthèse, soit : Si(,

En effet, la plage sur laquelle les positions doivent être repérées pour extraire les données, est soumise à condition. Les cellules vides doivent être exclues. Dans un raisonnement matriciel, ce critère peut être imbriqué pour restreindre le champ d'action.

• Désigner de nouveau la précédente plage de calcul par son nom, soit : idu,
• Puis, taper l'égalité suivante : ='',

Si des lignes vides sont identifiées, cela signifie que les valeurs n'ont pas été extraites. Elles ne sont donc pas uniques. Elles ne doivent pas être considérées.

• Taper un point-virgule (;) pour passer dans la branche Alors de la fonction Si,
• Saisir deux guillemets ('') pour ignorer la cellule,

Dans le cas contraire, nous savons qu'il s'agit des villes uniques extraites destinées à être regroupées. La fonction Equiv agissant champ à champ permet de déceler la position de ces correspondances, comme nous l'avons déjà démontré.

• Taper un point-virgule (;) pour passer dans la branche Sinon de la fonction Si,
• Saisir la fonction donnant les positions suivie d'une parenthèse, soit : Equiv(,
• Désigner la plage du calcul précédent par son nom, soit : idu,
• Taper un point-virgule (;) pour passer dans l'argument du tableau de recherche,
• Désigner de nouveau la précédente plage de calcul par son nom, soit : idu,
• Taper un point-virgule suivi du chiffre zéro, soit ;0, pour une recherche exacte,
• Puis, fermer la parenthèse de la fonction Equiv,
• Dans l'enchaînement, fermer la parenthèse de la fonction Si,

Grâce à la fonction Equiv comparant toutes les lignes des deux matrices, nous retournons les positions des cellules non vides, soit des villes uniques extraites. Ces positions doivent être identifiées par les rangs de la fonction Grande.Valeur pour que les données correspondantes soient extraites et regroupées. Pour cela, nous devons lui passer une matrice virtuelle d'une hauteur identique à la plage d'extraction. Ainsi, tous les rangs potentiels seront considérés.

• Taper un point-virgule (;) pour passer dans l'argument du rang de la fonction Grande.Valeur,
• Inscrire la fonction donnant la ligne d'une cellule, suivie d'une parenthèse, soit : Ligne(,

En guise de cellule, c'est une matrice que nous allons lui passer. Rappelez-vous, tous les rangs doivent être traités.

• Saisir la fonction d'interprétation suivie d'une parenthèse, soit : Indirect(,

En effet, la matrice à construire est virtuelle. Nous devons interpréter ses lignes.

• Définir la ligne de départ de cette dernière comme suit : '1:',

Nous définissons ainsi la borne supérieure débutant sur la première ligne. Il en résultera le premier rang, soit la première ville identifiée à retourner et regrouper avec les autres. Pour les considérer toutes, nous l'avons dit, nous devons définir sa hauteur sur celle de la matrice d'extraction.

• Inscrire le caractère de concaténation pour annoncer la borne inférieure,
• Saisir la fonction Lignes suivie d'une parenthèse, soit : Lignes(,

Cette dernière, contrairement à son homologue au singulier renseigne sur le nombre de lignes contenues dans une matrice qui lui est passée en paramètre. En lui passant la colonne du calcul, nous définirons la borne inférieure de la matrice virtuelle pour considérer tous les rangs.

• Désigner une fois encore la plage du précédent calcul par son nom, soit : idu,
• Fermer la parenthèse de la fonction Lignes,
• Fermer la parenthèse de la fonction Indirect,
• Fermer la parenthèse de la fonction Ligne,
• Fermer la parenthèse de la fonction Grande.Valeur,
• Fermer la parenthèse de la fonction Index,

En effet, comme nous le répétons à chaque occasion, la matrice d'extraction définie en premier argument de la fonction Index n'est constituée que d'une seule colonne. De fait, il n'est pas nécessaire de renseigner le troisième argument. L'extraction se fera naturellement dans cette rangée.

• Taper un point-virgule (;) pour passer dans le second argument de la fonction SiErreur,
• Inscrire deux guillemets ('') pour ignorer l'extraction en cas d'anomalie,
• Fermer la parenthèse de la fonction SiErreur,
• Enfin, valider nécessairement la formule matricielle par le raccourci CTRL + MAJ + Entrée,

Nous produisons bien l'extraction des villes uniques qui plus est, regroupées. Les cellules vides sont ignorées en raison des non correspondances dévoilées par la fonction Equiv. Les villes sont quant à elles restituées dans l'ordre des rangs correspondant à leurs positions. La formule matricielle d'extraction que nous avons construite est la suivante :

{=SIERREUR(INDEX(idu; GRANDE.VALEUR(SI(idu=''; ''; EQUIV(idu;idu;0)); LIGNE(INDIRECT('1:' & LIGNES(idu))))); '')}

Pour produire l'extraction regroupée des doublons, la technique est la même. Mais la cible change. C'est la matrice idd qui doit être considérée à la place de la matrice idu.

• Sélectionner toutes les cellules de la dernière colonne, soit la plage L4:L14,
• Adapter le précédent calcul matriciel comme suit :

{=SIERREUR(INDEX(idd; GRANDE.VALEUR(SI(idd=''; ''; EQUIV(idd; idd; 0)); LIGNE(INDIRECT('1:' & LIGNES(idd)))));'')}

• Puis, le valider par le raccourci clavier CTRL + MAJ + Entrée,

Nous produisons bien l'extraction regroupée des villes en double.