Extraire et grouper les valeurs communes à deux listes

Pour partager cette vidéo sur les réseaux sociaux ou sur un site, voici son url :


Sujets que vous pourriez aussi aimer :


Valeurs communes entre deux listes

Pour déceler et extraire les données identiques dans une comparaison de listes Excel, les calculs matriciels sont de nouveau nécessaires. Et nous allons le voir, les techniques que nousavons apprises lors de la formation précédente pour éliminer les trous dans les tableaux, vont s'avérer précieuses.



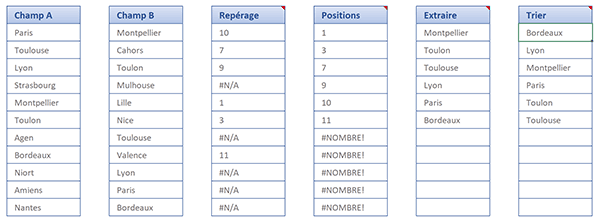
Dans l'exemple finalisé illustré par la capture ci-dessus, deux listes sont à comparer. Elles sont respectivement titrées Champ A et Champ B. La dernière colonne sur la droite est nommée Trier. Elle offre l'extraction avec organisation alphabétique croissante des données identiques issues deux premières colonnes.

Source et présentation du concept
Pour simplifier l'étude, nous proposons tout d'abord de récupérer des informations existantes.

• Télécharger le classeur liste-textes-communs.xlsx en cliquant sur ce lien,
• Double cliquer sur le fichier réceptionné pour l'ouvrir dans Excel,
• Puis, cliquer sur le bouton Activer la modification du bandeau de sécurité,

Vous remarquez la présence de quelques colonnes avant d'aboutir à la dernière, consistant à produire cette extraction ordonnée. Grâce à la puissance des calculs matriciels, nous pourrions très bien aboutir l'extraction des valeurs communes en une seule formule.



Mais pour la bonne compréhension, nous proposons de réaliser des calculs intermédiaires de repérage. Ensuite, nous imbriquerons ces syntaxes les unes dans les autres pour fournir la restitution dans la dernière colonne.

Si vous déployez la zone Nom en haut à gauche de la feuille Excel, vous notez que les deux premières colonnes sont identifiées par des intitulés.



Nous exploiterons ces noms pour simplifier la construction des formules matricielles.

Repérer les contenus identiques
Nous devons analyser les deux premiers champs dans un raisonnement matriciel. Chaque ligne d'une liste doit être comparée à toutes les valeurs de l'autre. Grâce à la nature de la fonction Equiv, il en résulte les positions des éléments concordants donc communs. Et pour ce faire, nous allons exploiter une technique strictement identique à celle de la formation précédente pour éliminer les trous dans une liste.

• Sélectionner toutes les cellules de la colonne Repérage, soit la plage F4:F14,
• Taper le symbole égal (=) pour initier la syntaxe de la formule matricielle,
• Inscrire la fonction trouvant les positions, suivie d'une parenthèse, soit : Equiv(,
• Désigner le premier champ à comparer par son nom, soit : champa,
• Taper un point-virgule (;) pour passer dans l'argument du tableau de recherche,
• Désigner le second champ à comparer par son nom, soit : champb,

Donc, en guise de valeur cherchée, nous fournissons la première colonne des villes. Puis, nous désignons la seconde colonne des villes comme tableau de recherche. Dans un raisonnement matriciel, ce sont toutes les lignes des deux champs qui vont être étudiées conjointement. De par sa nature, dès qu'une concordance sera trouvée, la fonction Equiv, livrera les positions concernées.

• Taper un point-virgule suivi du chiffre zéro, soit : ;0, pour réaliser une recherche exacte,
• Fermer la parenthèse de la fonction Equiv,
• Puis, valider nécessairement la formule matricielle par le raccourci CTRL + MAJ + Entrée,

C'est lui qui intime l'ordre de raisonner sur les lignes des matrices. D'ailleurs, vous pouvez constater la présence des accolades, encadrant la syntaxe, dans la barre de formule. Les positions apparaissent au milieu des erreurs révélant les non correspondances.



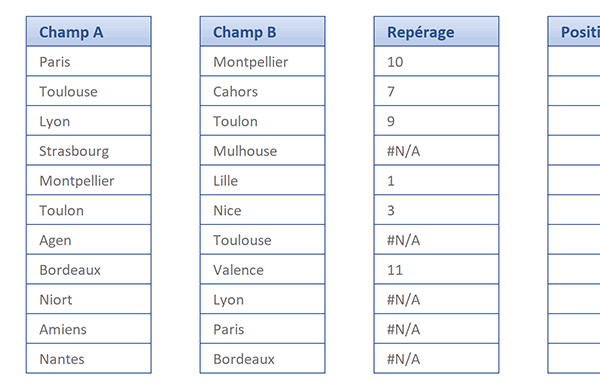
La ville de Paris, issue de la première rangée est bien située en dixième position du second champ. La ville de Toulouse est effectivement placée en septième position dans la seconde matrice.

La formule matricielle de repérage que nous avons construite, est la suivante :

{=EQUIV(champa;champb;0)}

Regrouper les positions identifiées
Ces positions calculées, nous devons les regrouper dans un second calcul matriciel intermédiaire. C'est ainsi que nous pourrons ensuite offrir l'extraction des valeurs communes réunies. Comme nous l'avons déjà appris, c'est donc la fonction Excel Petite.Valeur qui permet, dans un raisonnement matriciel, de regrouper toutes les positions trouvées, en fonction de leurs rangs. Mais ce calcul est soumis à condition. Pour isoler les numéros, les erreurs retournées par le précédent calcul, doivent être détectées. C'est pourquoi, nous devons employer la fonction logique EstNa, en guise de test.

• Sélectionner toutes les cellules de la colonne Positions, soit la plage H4:H14,
• Taper le symbole égal (=) pour débuter la construction de la formule matricielle,
• Taper la fonction pour les petites valeurs suivie d'une parenthèse, soit : Petite.Valeur(,
• Saisir la fonction conditionnelle suivie d'une parenthèse, soit : Si(,
• Inscrire la fonction logique de test, suivie d'une parenthèse, soit : EstNa(,
• Reproduire le même calcul que précédemment, soit : Equiv(champa;champb;0),

Ainsi, en guise de colonne d'extraction, nous fournissons à la fonction Petite.Valeur, une matrice conditionnelle. Si ce test est concluant, nous savons qu'une erreur est retournée signifiant que la correspondance entre des éléments communs n'est pas avérée. Dans ces conditions, nous devons ignorer le retour fourni par le calcul de la fonction Equiv.

• Fermer la parenthèse de la fonction EstNa,
• Taper un point-virgule (;) pour passer dans la branche Alors de la fonction Si,
• Inscrire deux guillemets ('') pour ignorer l'erreur,
• Taper un point-virgule (;) pour passer dans la branche Sinon de la fonction Si,

Lorsque le calcul des positions ne retourne pas d'anomalie, nous devons restituer ces dernières. Donc, nous devons de nouveau réaliser la même recherche.

• Reproduire de nouveau le même calcul de repérage, soit : Equiv(champa;champb;0),
• Puis, fermer la parenthèse de la fonction Si,
• Taper un point-virgule (;) pour passer dans l'argument du rang de la fonction Petite.Valeur,

Pour que toutes les positions soient prélevées dans l'ordre et toujours dans un raisonnement matriciel, nous devons construire une matrice virtuelle. Cette dernière doit être de la même hauteur que les champs analysés. Ainsi, toutes les positions seront considérées et extraites dans l'ordre.

• Inscrire la fonction pour la ligne d'une cellule, suivie d'une parenthèse, soit : Ligne(,
• Taper la fonction d'interprétation suivie d'une parenthèse, soit : Indirect(,
• Saisir le chiffre 1 suivi du symbole deux points entre guillemets, soit : '1:',

Ainsi et dans l'optique de cette matrice virtuelle, en guise de rangs multiples, nous annonçons le point de départ, situé sur la première rangée. Le symbole deux points annonce la venue de la borne inférieure que nous devons lui adjoindre.

• Inscrire le caractère de concaténation (&) pour associer la borne inférieure,
• Taper la fonction donnant le nombre de lignes d'une plage, avec une parenthèse, soit : Lignes(,
• Désigner le second champ par son nom, soit : champb,

Ainsi nous fournissons la borne inférieure de la matrice virtuelle, régie par le nombre de lignes contenues dans la deuxième colonne des villes. De fait, nous construisons une matrice de même hauteur, capable de passer en revue toutes les positions extraites, par raisonnement matriciel.

• Fermer la parenthèse de la fonction Lignes,
• Fermer la parenthèse de la fonction Indirect,
• Fermer la parenthèse de la fonction Ligne,
• Fermer la parenthèse de la fonction Petite.Valeur,
• Enfin, valider nécessairement la formule matricielle par le raccourci CTRL + MAJ + Entrée,

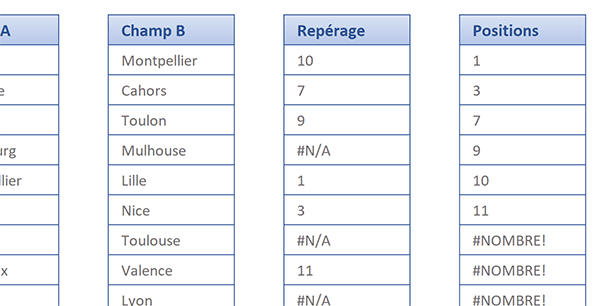
Comme vous le constatez, toutes les positions trouvées sont extraites. Mais de plus, elles sont réunies et triées par ordre croissant. La formule matricielle que nous avons bâtie est la suivante :

{=PETITE.VALEUR(SI(ESTNA(EQUIV(champa; champb; 0)); ''; EQUIV(champa; champb; 0)); LIGNE(INDIRECT('1:' & LIGNES(champb))))}

Extraire les données identiques
Les numéros que nous venons de regrouper donnent les positions des villes identiques à extraire. Ce précédent calcul doit donc être intégré dans la fonction d'extraction Index. Elle doit réaliser sa recherche dans la deuxième colonne nommée champb pour restituer toutes les données situées aux positions trouvées.

• Copier la syntaxe du précédent calcul par sa barre de formule, sans le symbole égal,
• Penser à le revalider par le raccourci matriciel pour ne pas l'endommager,
• Sélectionner toutes les cellules de la troisième colonne de calcul, soit la plage J4:J14,
• Taper le symbole égal (=) pour débuter la syntaxe de la formule matricielle,
• Inscrire la fonction de gestion d'anomalie, suivie d'une parenthèse, soit : SiErreur(,

En effet, nous devons neutraliser les erreurs (#Nombre!) retournées en bout de course par la précédente formule.

• Saisir la fonction d'extraction suivie d'une parenthèse, soit : Index(,
• Désigner le second champ par son nom, soit : champb,
• Taper un point-virgule (;) pour passer dans l'argument des indices de lignes,
• Coller la syntaxe précédemment copiée, soit :

PETITE.VALEUR(SI(ESTNA(EQUIV(champa; champb; 0)); ''; EQUIV(champa; champb; 0)); LIGNE(INDIRECT('1:' & LIGNES(champb))))

C'est en effet ce calcul qui repère toutes les positions en ligne des villes communes à extraire.

• Fermer la parenthèse de la fonction Index,

La recherche est réalisée sur une unique rangée définie par la colonne champb passée en premier paramètre de la fonction Index. De fait, il n'est pas nécessaire de lui indiquer l'indice de colonne pour procéder à l'extraction. La fonction Index pointera implicitement et naturellement sur cette unique rangée.

• Taper un point-virgule (;) pour passer dans le second argument de la fonction SiErreur,
• Inscrire deux guillemets ('') pour conserver les résultats vierges en cas d'anomalie détectée,
• Fermer la parenthèse de la fonction SiErreur,
• Puis, valider nécessairement la formule matricielle par le raccourci CTRL + MAJ + Entrée,

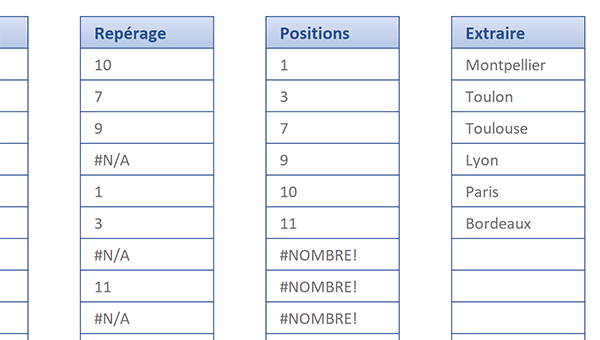
Nous obtenons bien l'extraction des villes communes aux deux rangées. De plus, les résultats sont purgés des anomalies générées par les calculs matriciels intermédiaires. Cette unique formule matricielle suffit à produire directement l'extraction convoitée. Elle imbrique en effet les deux précédentes formules selon la syntaxe suivante :

{=SIERREUR(INDEX(champb; PETITE.VALEUR(SI(ESTNA(EQUIV(champa; champb; 0)); ''; EQUIV(champa; champb; 0)); LIGNE(INDIRECT('1:' & LIGNES(champb))))); '')}

Trier les valeurs communes extraites
Pour terminer, nous souhaitons classer ces résultats textuels d'extraction par ordre alphabétique croissant. Pour cela, nous suggérons de répliquer une technique que nous avons démontrée dans une formation précédente. Elle consiste à exploiter la fonction Grande.Valeur dans un raisonnement forcément matriciel. Mais en guise de plage de cellules, nous souhaitons comparer entre eux tous les textes extraits grâce à la fonction Nb.Si. Chaque texte dépassé le plus grand nombre de fois par les autres, sera considéré comme le premier à classer dans la liste. Comme toujours ces positions doivent être dévoilées par la fonction Equiv. Et ces positions doivent être exploitées par la fonction Index pour produire l'extraction finale ordonnée.

• Sélectionner toutes les cellules de la dernière colonne, soit la plage L4:L14,
• Taper le symbole égal (=) pour initier la formule matricielle,
• Inscrire la fonction d'extraction suivie d'une parenthèse, soit : Index(,
• Sélectionner les cellules du précédent calcul, soit la plage J4:J14,
• Taper un point-virgule (;) pour passer dans l'argument des lignes à ordonner,
• Saisir la fonction trouvant ces positions, suivie d'une parenthèse, soit : Equiv(,
• Saisir la fonction des grandes valeurs, suivie d'une parenthèse, soit : Grande.Valeur(,
• Inscrire la fonction de dénombrement conditionnel, suivie d'une parenthèse, soit : Nb.Si(,

C'est dans cet argument de la plage à analyser que nous devons en effet évaluer les textes plus petits que les autres, dans la hiérarchie alphabétique. Grâce au raisonnement matriciel, nous allons pouvoir comparer chaque ville précédemment extraite avec toutes les autres. A l'instar des comparaisons numériques, l'opérateur d'inégalité considère que la lettre a est la plus petite tandis que la lettre z est la plus grande.

• Désigner de nouveau la plage des extractions précédentes, soit : J4:J14,
• Taper un point-virgule (;) pour passer dans l'argument du critère à compter,
• Saisir l'inégalité suivante entre guillemets : '>=',
• Inscrire le caractère de concaténation (&) pour poursuivre l'expression du critère,
• Désigner encore la précédente plage d'extraction, soit : J4:J14,
• Fermer la parenthèse de la fonction Nb.Si,

Grâce à ce dénombrement matriciel, nous connaîtrons les villes les plus souvent dépassées par les autres, dans l'ordre alphabétique. Il s'agit alors de les restituer dans l'ordre croissant. C'est la nature même de la fonction Grande.Valeur. En guise de rang, nous allons lui indiquer une matrice virtuelle de la même hauteur que la rangée d'extraction. Ainsi, tous les dénombrements seront pris dans l'ordre décroissant. Il en résultera une restitution des villes dans l'ordre croissant.

• Taper un point-virgule (;) pour passer dans l'argument du rang de la fonction Grande.Valeur,
• Saisir la fonction pour la ligne d'une cellule, suivie d'une parenthèse, soit : Ligne(,
• Inscrire la fonction d'interprétation suivie d'une parenthèse, soit : Indirect(,
• Saisir la première borne de la plage comme suit : '1:',

Nous sommes en train de construire une matrice virtuelle de même hauteur afin d'analyser tous les rangs permettant la restitution ordonnée. Le chiffre 1 désigne la première ligne de cette plage. Le symbole deux points (:) annonce la borne inférieure à suivre. Elle est dynamique. Elle dépend du nombre de lignes de la plage analysée. Nous devons la concaténer.

• Inscrire le caractère de concaténation (&),
• Saisir la fonction comptant les lignes d'une plage suivie d'une parenthèse, soit : Lignes(,
• Désigner les cellules du précédent calcul, soit la plage J4:J14,
• Fermer la parenthèse de la fonction Lignes,
• Fermer la parenthèse de la fonction Indirect,
• Fermer la parenthèse de la fonction Ligne,
• Fermer la parenthèse de la fonction Grande.Valeur,
• Taper un point-virgule (;) pour l'argument du tableau de recherche de la fonction Equiv,

Pour une restitution ordonnée, cette matrice doit correspondre strictement à la plage précédemment dénombrée conditionnellement.

• Répliquer le précédent calcul de dénombrement, soit : Nb.Si(J4:J14;'>='& J4:J14),
• Taper un point-virgule suivi du chiffre zéro, soit : ;0, pour une recherche exacte,
• Fermer la parenthèse de la fonction Equiv puis, fermer la parenthèse de la fonction Index,
• Enfin, valider la formule matricielle par le raccourci clavier CTRL + MAJ + Entrée,

Comme vous le constatez nous avons parfaitement réussi à classer les villes communes, issues de l'extraction précédente. Ce sont encore une fois les calculs matriciels qui autorisent ces prouesses.



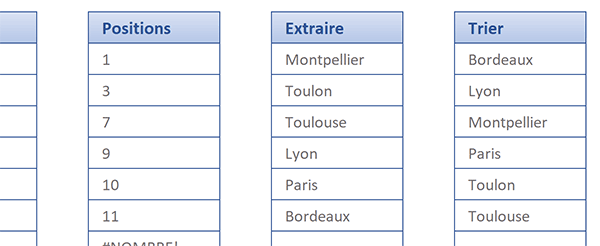
La formule matricielle que nous avons construite est la suivante :

{=INDEX(J4:J14; EQUIV(GRANDE.VALEUR(NB.SI(J4:J14;'>=' & J4:J14);LIGNE(INDIRECT('1:' & LIGNES(J4:J14)))); NB.SI(J4:J14;'>=' & J4:J14); 0))}