Eliminer les trous dans les listes Excel

Pour partager cette vidéo sur les réseaux sociaux ou sur un site, voici son url :


Sujets que vous pourriez aussi aimer :


Recréer des listes sans trous

Il arrive que nous ayons à traiter les données de tableaux mal formés. Ceux-ci peuvent avoir des trous, soit des rangées vierges intercalées. L'une des explications provient de la suppression d'enregistrements dans une base de données mal calibrée, n'éliminant pas les dépendances.



Dans l'exemple illustré par la capture ci-dessus, le tableau de gauche correspond à une source importée. Il présente des trous. Ces lignes vides intempestives sont supprimées par calcul matriciel dans le tableau de droite. Il restitue alors le contenu exact purgé des anomalies.

Source et présentation
Pour mener à bien ces travaux, nous proposons de réceptionner cette source imparfaite.

• Télécharger le classeur eliminer-trous-listes-excel.xlsx en cliquant sur ce lien,
• Double cliquer sur le fichier téléchargé pour l'ouvrir dans Excel,
• Puis, cliquer sur le bouton Activer la modification du bandeau de sécurité,

Le tableau de gauche énumère des activités situées dans des villes. On y aperçoit des lignes vides intercalées de ci et de là. Le tableau de droite est vierge. Il doit recomposer ce premier tableau en éliminant ces trous.



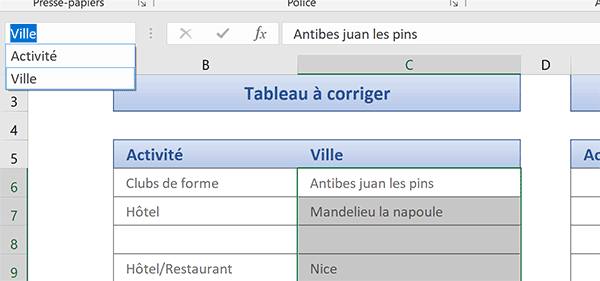
Si vous déployez la liste déroulante de la zone Nom, en haut à gauche de la feuille Excel, vous notez que les deux colonnes du tableau sont nommées en fonction de leurs titres. Nous exploiterons ces noms dans la construction des formules matricielles.

Identifier les lignes non vides
La nature de la fonction Equiv est de renvoyer la position des données cherchées. Encadrée dans un raisonnement matriciel, elle est capable d'analyser les lignes respectives des colonnes impliquées. L'idée consiste à lui demander de chercher toutes les activités dans la plage même des activités. A chaque fois qu'une concordance est trouvée, une position doit être retournée.

• Sélectionner toutes les activités du deuxième tableau, soit la plage de cellules E6:E42,
• Taper le symbole égal (=) pour initier la formule matricielle,
• Saisir la fonction de recherche suivie d'une parenthèse, soit : Equiv(,
• Désigner la plage des activités par son nom, soit Activité, en guise d'élément de recherche,
• Taper un point-virgule (;) pour passer dans l'argument de la colonne de recherche,
• Désigner de nouveau la plage des activités par son nom, soit : Activité,

De cette manière, toujours dans le processus matriciel, nous allons chercher chaque activité concordante dans leur propre plage. Pour chaque ligne de texte, l'égalité doit être avérée. Donc une position doit en résulter.

• Taper un point-virgule (;) suivi du chiffre zéro, soit : ;0, pour réaliser une recherche exacte,
• Fermer la parenthèse de la fonction Equiv,
• Puis, valider la formule matricielle par le raccourci clavier CTRL + MAJ + Entrée,

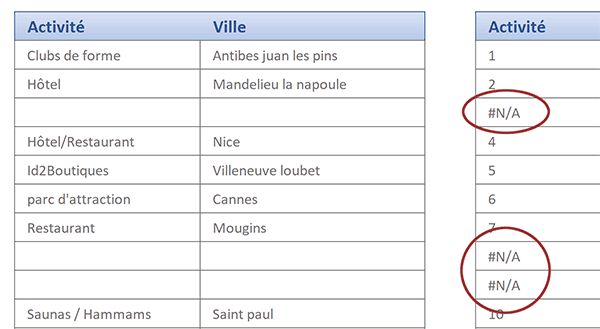
Comme vous pouvez le voir, grâce à cette formule matricielle, chaque texte est repéré par sa position. Dans le même temps, chaque cellule vide est identifiée par une erreur retournée par la fonction Equiv.

Extraire les données regroupées
Pour réaliser cette extraction, nous devons imbriquer la fonction Equiv dans la fonction Index. Comme vous le savez, elle permet de restituer la donnée située au croisement d'une ligne et d'une colonne. Ces indices de ligne nous les connaissons désormais grâce au précédent calcul. Mais un test doit être réalisé pour exclure toutes les cellules vides répondant par une erreur. Pour cela, nous devons exploiter la fonction logique EstNa dans une fonction conditionnelle Si. De plus, pour réaliser l'extraction groupée dans l'ordre des numéros, nous devons utiliser la fonction Petite.Valeur dans un raisonnement matriciel. Pour cela, en guise de rang, nous devons lui passer une matrice virtuelle de même hauteur que le tableau. C'est ainsi que toutes les positions seront recoupées tour à tour.

• Sélectionner tous les précédents calculs, soit la plage de cellules E6:E42,
• Enfoncer la touche Suppr du clavier pour les effacer,
• Puis, taper le symbole égal (=) pour initier la nouvelle formule matricielle,
• Inscrire la fonction d'extraction suivie d'une parenthèse, soit : Index(,
• Désigner la colonne des activités par son nom, soit : Activité,
• Taper un point-virgule (;) pour passer dans l'argument des lignes à trouver,
• Saisir la fonction trouvant les petites valeurs, suivie d'une parenthèse, soit : Petite.Valeur(,
• Inscrire la fonction conditionnelle suivie d'une parenthèse, soit : Si(,
• Taper la fonction logique de test d'erreur suivie d'une parenthèse, soit : EstNa(,
• Répliquer strictement le même calcul que précédemment, soit : Equiv(Activité;Activité;0),

De cette manière, grâce à la fonction EstNa imbriquée dans le critère de la fonction Si, nous sommes en train de tester chaque élément retournant une erreur à la place d'une position. C'est ainsi que nous allons pouvoir exclure les lignes vides de la restitution. Nous sommes en effet dans les bornes de la fonction Petite.Erreur qui va rapatrier seulement les éléments identifiés par des rangs, correspondant aux positions.

• Fermer la parenthèse de la fonction EstNa,
• Taper un point-virgule (;) pour passer dans la branche Alors de la fonction Si,
• Saisir deux guillemets ('') pour ignorer les cellules vides identifiées par des erreurs,
• Taper un point-virgule (;) pour passer dans la branche Sinon de la fonction Si,
• Saisir de nouveau le même calcul matriciel pour les positions, soit : Equiv(Activité;Activité;0),

Ainsi, lorsqu'aucune erreur n'est générée, nous spécifions clairement la plage reconnue par les positions identifiées par le calcul. Nous devons maintenant exploiter ces positions pour extraire les textes dans l'ordre.

• Fermer la parenthèse de la fonction Si,
• Taper un point-virgule (;) pour passer dans le rang de la fonction Petite.Valeur,
• Taper la fonction pour la ligne d'une cellule, soit Ligne(,
• Inscrire la fonction d'interprétation suivie d'une parenthèse, soit : Indirect(,

En effet, pour passer en revue tous les rangs identifiés par les positions calculées, nous devons construire une matrice virtuelle. Celle-ci doit être de la même hauteur que le tableau d'origine. C'est ainsi que toutes les positions potentielles pourront être considérées tour à tour dans ce raisonnement matriciel.

• Taper la borne supérieure entre guillemets, comme suit : '1:',
• Inscrire le caractère de concaténation pour annoncer la borne inférieure à suivre,
• Taper la fonction pour le nombre de lignes d'une plage, suivie d'une parenthèse, soit : Lignes(,

Attention, il ne s'agit pas de la même fonction que précédemment. Elle est d'ailleurs judicieusement orthographiée au pluriel.

• Désigner la colonne des activités par son nom, soit : Activité,

Ainsi, nous construisons une matrice virtuelle débutant de la première ligne et s'étendant sur autant de lignes que celles contenues dans la colonne en cours d'étude. Dans un raisonnement matriciel, tous ces indices seront considérés tour à tour sous forme de rang. Ces rangs permettront d'extraire les textes aux positions identifiées par la fonction Equiv.

• Fermer la parenthèse de la fonction Lignes,
• Fermer la parenthèse de la fonction Indirect,
• Fermer la parenthèse de la fonction Ligne,
• Fermer la parenthèse de la fonction Petite.Valeur,
• Puis, Fermer la parenthèse de la fonction Index,

Nous ne prenons pas soin de renseigner l'argument de la colonne pour la fonction Index. En effet, la matrice de recherche désignée en premier argument est matérialisée par une seule colonne. En conséquence, la fonction Index piochera naturellement les données dans cette dernière.

• Valider la formule matricielle par le raccourci clavier CTRL + MAJ + Entrée,

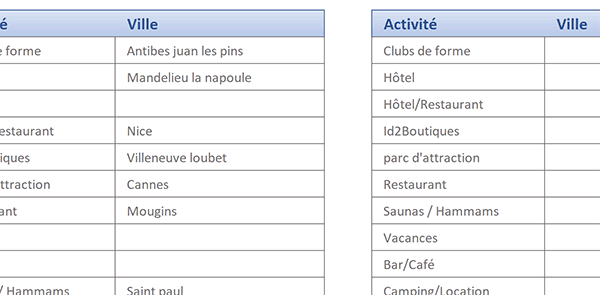
Comme vous pouvez le voir, nous obtenons les résultats extraits du premier tableau et regroupés. Les cellules vides ont toutes été éliminées car ignorées grâce au test logique sur l'erreur générée.

Néanmoins, vous notez la présence d'anomalies en bout de tableau (#Nombre). La raison est simple, en l'absence des cellules vides, plus aucune position n'étant repérée, la fonction Petite.Valeur ne peut produire aucun résultat. Pour les neutraliser, il suffit de corriger la syntaxe en l'intégrant dans la fonction SiErreur, comme suit :

{=SiErreur(INDEX(Activité; PETITE.VALEUR(SI(ESTNA(EQUIV(Activité; Activité; 0)); ''; EQUIV(Activité; Activité; 0)); LIGNE(INDIRECT('1:' & LIGNES(Activité))))); '')}

De la même façon, pour réaliser l'extraction groupée de villes, il suffit d'adapter la matrice concernée dans la formule matricielle, comme suit :

{=SIERREUR(INDEX(Ville; PETITE.VALEUR(SI(ESTNA(EQUIV(Ville; Ville; 0)); ''; EQUIV(Ville; Ville; 0)); LIGNE(INDIRECT('1:'& LIGNES(Ville))))); '')}