Extraire les valeurs uniques dans l'ordre

Pour partager cette vidéo sur les réseaux sociaux ou sur un site, voici son url :


Sujets que vous pourriez aussi aimer :


Créer des listes sans doublons

Extraire les valeurs uniques d'une liste constituée de doublons en une seule formule, voici l'objectif des démonstrations à suivre.



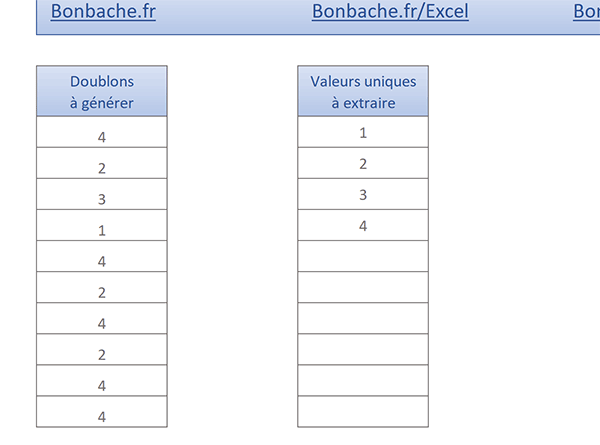
Dans l'exemple illustré par la capture, la liste de gauche offre une série de nombres avec des redondances. Celle de droite, extirpe les chiffres uniques réorganisés dans l'ordre croissant. Et c'est une fois encore un raisonnement matriciel qui permet de résoudre le cas.

Source à télécharger
Bien que les travaux puissent s'établir à partir d'un classeur vierge, nous proposons de réceptionner une structure existante.

• Télécharger le classeur extraire-valeurs-uniques-triees.xlsx en cliquant sur ce lien,
• Double cliquer sur le fichier réceptionné pour l'ouvrir dans Excel,
• Puis, cliquer sur le bouton Activer la modification du bandeau de sécurité,

Nous réceptionnons une feuille vierge de données. Cependant, deux rangées sont formatées sur quelques lignes. Dans la première, nous devons générer des chiffres avec des répétitions. Dans la seconde, nous devons en extraire les valeurs uniques triées.

• Sélectionner la plage de cellules B4:B13,

En consultant la zone Nom en haut à gauche de la feuille, vous constatez que cette plage est identifiée par un intitulé (Liste). Nous exploiterons ce nom pour simplifier la syntaxe de la formule d'extraction.



Générer aléatoirement des répétitions
Avant de chercher à établir la formule capable d'extraire les valeurs uniques, nous devons proposer une liste offrant des redondances. La plage nommée Liste est constituée de 10 cellules. Il suffit donc d'y générer des nombres aléatoires entiers inférieurs à 10 pour être certain de créer des doublons. Nous connaissons la fonction appropriée. Elle se nomme Alea.Entre.Bornes. Elle attend deux paramètres. Il s'agit de la borne inférieure puis de la borne supérieure.

• Sélectionner de nouveau la plage de cellules B4:B13,
• Saisir la formule suivante : =Alea.Entre.Bornes(1;5),
• Puis, valider le calcul par le raccourci clavier CTRL + Entrée,

Cette technique permet de répliquer la logique sur l'ensemble de la plage présélectionnée.



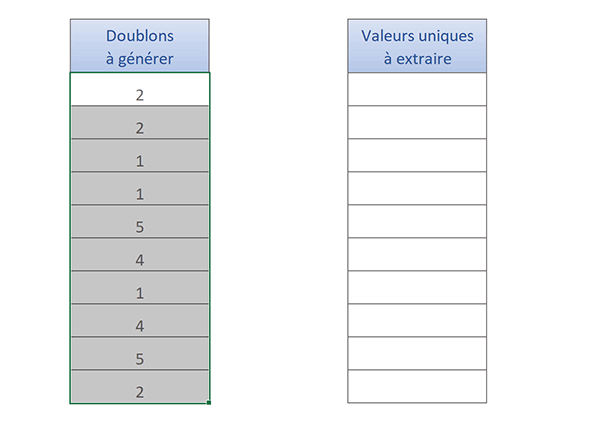
Nous obtenons bien une série de nombres entiers dotée de répétitions. Mais à ce stade, ils sont liés à la formule. En conséquence, à chaque événement généré sur la feuille, ils vont être recalculés. Nous devons les délier du calcul.

• Sélectionner de nouveau la plage de cellules B4:B13,
• La copier à l'aide du raccourci clavier CTRL + C par exemple,
• Sélectionner alors uniquement la première case de la rangée, soit la cellule B4,
• Coller la précédente sélection à l'aide du raccourci clavier CTRL + V par exemple,
• Cliquer ensuite sur la flèche de la balise active qui se déclenche en bas de la sélection,
• Dans la liste des propositions, cliquer sur l'icône Valeurs,

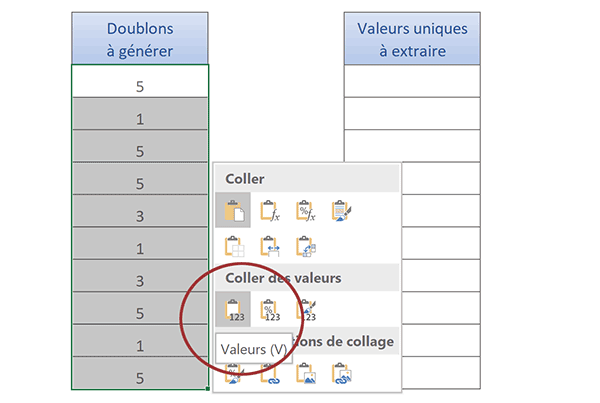
Les nombres se génèrent une dernière fois. Mais ils sont désormais dissociés de la formule. Ils sont donc figés avec leurs répétitions.

Extraire les valeurs uniques classées
Seul un calcul matriciel, capable de raisonner sur l'ensemble du tableau, est en mesure d'analyser l'ensemble des données afin d'en fournir une synthèse purgée sur la base d'une seule formule. L'idée consiste à passer en revue l'ensemble des nombres de la liste en repérant leurs positions grâce à la fonction Equiv. Ces positions doivent être analysées sur une hauteur équivalente à celle du tableau. Nous exploiterons la fonction Ligne dans un schéma matriciel pour les considérer toutes à la fois. Sur ces positions repérées, seules les valeurs uniques doivent être extraites. L'astuce consiste à englober toute la syntaxe dans la fonction Petite.Valeur sur un rang qui évolue en fonction de la hauteur de cette liste.

• Sélectionner toute la plage des valeurs à extraire, soit la plage de cellules D4:D13,
• Taper le symbole égal (=) pour initier la formule matricielle,
• Saisir la fonction de gestion d'anomalie, suivie d'une parenthèse, soit : SiErreur(,

En effet, nous n'obtiendrons jamais autant de valeurs uniques qu'il y en a dans la liste d'origine. Pour éviter que la formule retourne une erreur en bout de course, nous choisissons de gérer ces exceptions.

• Saisir la fonction suivante, suivie d'une parenthèse : Petite.Valeur(,

Dans sa version classique, sur une plage de cellules mentionnée en premier argument, elle permet d'extraire l'une des petites valeurs, selon le rang indiqué en second paramètre. Mais en guise de plage de cellules, nous allons lui passer un critère matriciel. Et en guise de rang, nous allons lui passer toutes les valeurs qui honorent la hauteur de la liste source. Il en résultera toutes les valeurs uniques triées par ordre croissant, de la plus petite à la plus grande donc.

• Saisir la fonction conditionnelle suivie d'une parenthèse, soit : Si(,
• Taper la fonction pour la position d'une valeur cherchée, suivie d'une parenthèse, soit : Equiv(,
• Désigner les chiffres générés par le nom attribué à la plage, soit : Liste,
• Taper un point-virgule (;) pour passer dans l'argument de la colonne de recherche,
• Désigner de nouveau la même plage par son nom, soit : Liste,

Dans ce protocole matriciel, nous cherchons donc toutes les positions des valeurs de la plage dans la plage elle-même. C'est le critère que nous allons poser qui va permettre de ne conserver que les valeurs uniques. Il consiste à établir la correspondance de la position avec la ligne en cours d'analyse. Souvenez-vous en effet, une fonction de recherche s'arrête sur la première occurrence concordante trouvée.

• Taper un point-virgule suivi du chiffre zéro, soit : ;0, pour une recherche exacte,
• Fermer la parenthèse de la fonction Equiv,
• Taper le symbole égal (=) pour annoncer la condition à honorer,
• Saisir la fonction pour la ligne d'une cellule suivie d'une parenthèse, soit : Ligne(,
• Saisir la fonction d'interprétation de plage suivie d'une parenthèse, soit : Indirect(,
• Saisir le chiffre 1 suivi du symbole deux points entre guillemets, soit : '1:',

Nous initions ainsi le point de départ de la plage virtuelle. Il reste à définir sa borne inférieure de sorte qu'elle soit de la même hauteur que la liste des données numériques. C'est ainsi que le processus matriciel, analysant les lignes respectives des matrices, peut s'enclencher.

• Taper le symbole de concaténation, soit : &,
• Saisir la fonction suivante, suivie d'une parenthèse : Lignes(,

Elle ne doit pas être confondue avec son homologue au singulier. Cette fonction retourne le nombre de lignes d'une plage qui lui est passée en argument.

• Désigner la plage des nombres par son nom, soit : Liste,
• Fermer la parenthèse de la fonction Lignes,
• Fermer la parenthèse de la fonction Indirect,
• Puis, fermer la parenthèse de la fonction Ligne,

Grâce à cette construction, nous scrutons dans la comparaison, tous les indices de position, sur une hauteur de plage fidèle à la source.

• Taper un point-virgule (;) pour passer dans la branche Alors de la fonction Si,
• Désigner de nouveau la matrice des chiffres par son nom, soit : Liste,
• Puis, fermer la parenthèse de la fonction Si,

Observons un arrêt le temps d'une explication nécessaire à la bonne compréhension. Toutes les lignes de la matrice des chiffres et de la matrice virtuelle vont être analysées respectivement. Lorsqu'une position coïncide avec un chiffre, celui-ci est conservé. Mais lorsqu'il s'agit d'une répétition, étant donné que la fonction Equiv s'arrête sur la première valeur, les positions ne coïncident plus. Donc le chiffre redondant est exclu. C'est alors la fonction Petite.Valeur qui doit se charger du classement, selon l'ordre matriciel que nous allons lui fournir. De même, vous avez remarqué que nous n'avons pas pris soin de renseigner la branche Sinon de la fonction Si. Seules les concordances nous intéressent. Pour le reste, les anomalies doivent être gérées par la fonction SiErreur.

• Taper un point-virgule (;) pour passer dans l'argument du rang de la fonction Petite.Valeur,
• Copier la matrice virtuelle précédente, soit : Ligne(Indirect('1:'&Lignes(Liste))),

C'est ainsi que nous lui indiquons tous les rangs à respecter dans l'ordre, en partant du premier, soit du plus petit.

• Fermer la parenthèse de la fonction Petite.Valeur,
• Taper un point-virgule (;) pour passer dans l'argument de la gestion d'erreur,
• Saisir deux guillemets ('') pour garder la cellule vide en cas d'anomalie,
• Fermer la parenthèse de la fonction SiErreur,
• Enfin, valider nécessairement la formule par le raccourci clavier CTRL + MAJ + Entrée,

Toutes les valeurs uniques sont parfaitement extraites, triées dans l'ordre croissant qui plus est.



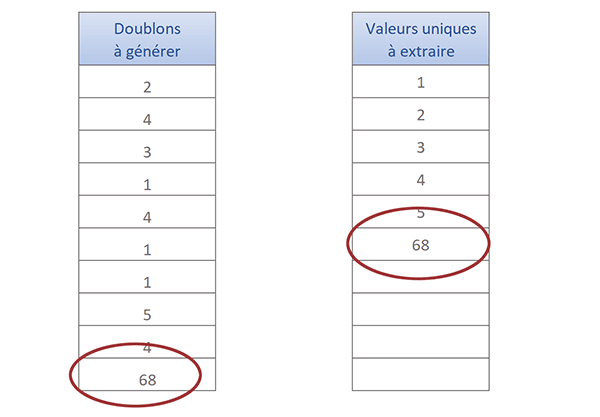
Et si vous choisissez d'ajouter une nouvelle valeur, en queue de liste par exemple, vous constatez qu'elle est immédiatement rapatriée dans l'extraction des données uniques. La formule matricielle que nous avons bâtie est la suivante :

{=SIERREUR(PETITE.VALEUR(SI(EQUIV(liste; liste; 0)=LIGNE(INDIRECT('1:'&LIGNES(liste))); liste); LIGNE(INDIRECT('1:'&LIGNES(liste)))); '')}

Pour un tri décroissant, il suffit naturellement de remplacer la fonction Petite.Valeur par la fonction Grande.Valeur. Du fait de la nature de ces fonctions, ces extractions ne sont possibles que sur des valeurs numériques. Mais une fois les chiffres extraits, il est très simple d'associer les textes correspondants, en réalisant une recherche des positions grâce aux fonctions Index et Equiv. Ce sont des notions que nous avons démontrées à maintes reprises, notamment au travers de la formation Excel pour extraire sur des critères recoupés.