Trier les nombres sans vides par formule matricielle

Pour partager cette vidéo sur les réseaux sociaux ou sur un site, voici son url :


Sujets que vous pourriez aussi aimer :


Trier les nombres par calcul

Les formules matricielles permettent de nombreuses prouesses comme celles d'organiser les nombres tout en excluant les cellules vides et ce, à l'aide d'une seule formule. Lorsque les données textuelles ne sont pas à considérer, la syntaxe s'allège considérablement. Nous allons le constater. Et forcément, cette solution permet de réorganiser plus facilement les données attachées dans une source d'informations dynamique.



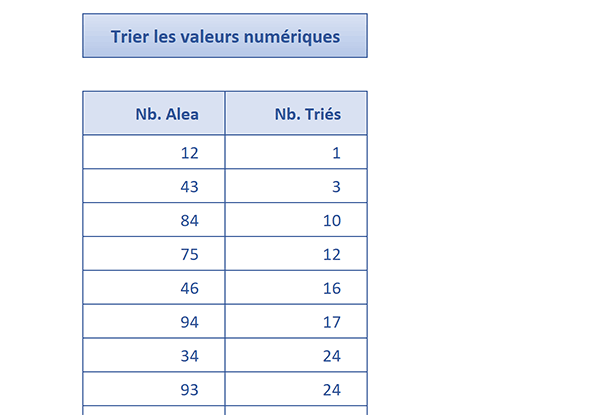
Dans l'exemple illustré par la capture, l'organisation croissante des nombres est réalisée dans la colonne de droite par rapport à une série de valeurs désorganisées dans la colonne de gauche.

Source et présentation
Pour la construction de cette formule, nous proposons de récupérer une source offrant cette liste de nombres.

• Télécharger le classeur trier-nombres-sans-vides.xlsx en cliquant sur ce lien,
• Double cliquer sur le fichier téléchargé pour l'ouvrir dans Excel,
• Puis, cliquer sur le bouton Activer la modification du bandeau de sécurité,

Nous retrouvons donc cette liste de nombres aléatoires et non triés en colonne B.



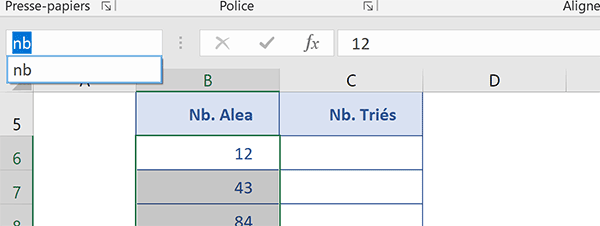
En déployant la zone Nom, en haut à gauche de la feuille Excel, vous notez que cette colonne porte l'intitulé nb. Nous l'utiliserons dans la formule matricielle pour désigner ces valeurs numériques à réorganiser.

Trier par formule matricielle
L'organisation des données numériques est triviale dans un raisonnement matriciel. Il s'agit d'exploiter la fonction Excel Petite.Valeur. En exerçant cette dernière sur l'intégralité de la matrice des nombres pour considérer tous les rangs possibles, il en résulte l'extraction de ces derniers triés du plus petit au plus grand.

• Sélectionner toutes les cellules de la seconde colonne, soit la plage C6:C25,
• Taper le symbole égal (=) pour initier la formule matricielle,
• Inscrire la fonction de gestion des anomalies, suivie d'une parenthèse, soit : SiErreur(,

De cette manière, en cas de nombre absent car supprimé, nous neutraliserons les messages d'erreur.

• Saisir la fonction pour le tri matriciel, suivie d'une parenthèse, soit : Petite.Valeur(,
• Désigner la matrice des valeurs numériques par son nom, soit : nb,
• Taper un point-virgule (;) pour passer dans l'argument du rang de la fonction Petite.Valeur,

Ce paramètre est particulièrement important pour notre réalisation. Nous sommes dans un raisonnement matriciel. Nous analysons donc globalement les données des colonnes impliquées. Ici, il n'y en a qu'une. En guise de rang unique, nous allons lui fournir une matrice virtuelle de même hauteur que le tableau et débutant à partir de la première ligne. De fait, tous les rangs, donc toutes les positions vont être analysées. La première va être attribuée au nombre le plus petit, la deuxième au suivant et ainsi de suite.

• Inscrire la fonction donnant la ligne d'une cellule, suivie d'une parenthèse, soit : Ligne(,

Nous le répétons, nous sommes dans un raisonnement matriciel. Nous n'allons donc pas lui fournir une cellule mais une matrice contenant autant de cellules que le tableau. Elle ne va donc pas retourner qu'un seul indice de ligne. Tous vont être retournés. Il va en résulter les positions sous forme de rang pour l'organisation du tri croissant. En revanche, cette matrice doit être construite de toutes pièces. Nous devons donc l'interpréter.

• Inscrire la fonction d'interprétation suivie d'une parenthèse, soit : Indirect(,
• Taper le point de départ de la matrice entre guillemets, comme suit : '1:',

Ainsi, nous définissons bien le point de départ sur la première ligne pour retourner le premier rang, soit la première position. Les deux points annoncent la borne inférieure à suivre. Celle-ci est dynamique. Nous devons la calculer en fonction du nombre d'éléments contenus dans le tableau.

• Inscrire le caractère de concaténation (&) pour l'assemblage à suivre,
• Inscrire la fonction donnant le nombre de lignes, suivie d'une parenthèse, soit : Lignes(,

Attention, contrairement à son homologue, cette fonction est au pluriel. Elle ne retourne pas la même information.

• Désigner de nouveau la matrice des nombres par son nom, soit : nb,
• Fermer la parenthèse de la fonction Lignes,
• Fermer la parenthèse de la fonction Indirect,
• Fermer la parenthèse de la fonction Ligne,
• Puis, fermer la parenthèse de la fonction Petite.Valeur,
• Taper un point-virgule (;) pour passer dans le second argument de la fonction SiErreur,
• Inscrire deux guillemets ('') pour ignorer le résultat en cas d'anomalie,
• Fermer la parenthèse de la fonction SiErreur,
• Enfin, valider nécessairement la formule matricielle par le raccourci CTRL + MAJ + Entrée,

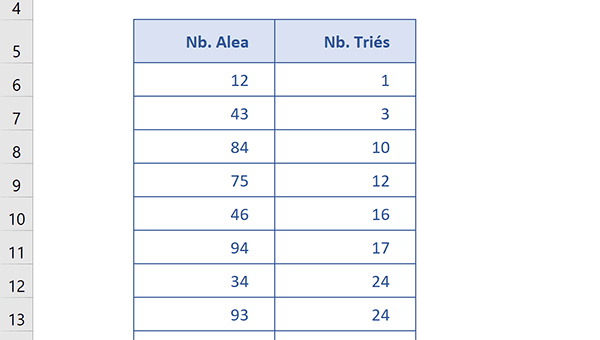
Toutes les données numériques sont effectivement parfaitement réorganisées. Les nombres sont désormais triés par ordre croissant. Et si vous modifiez des valeurs ou supprimez l'une d'entre elles comme le chiffre 1 en ligne 15, vous constatez que la liste triée se réorganise automatiquement.





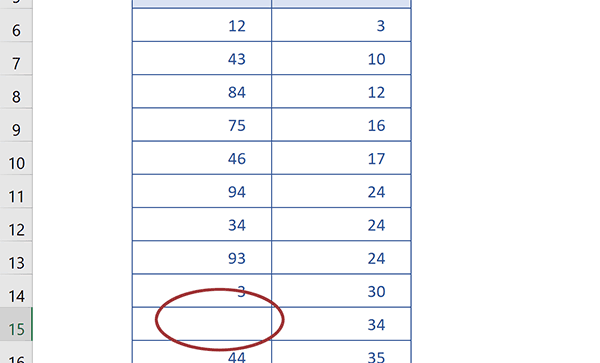
La formule matricielle de tri que nous avons construite est la suivante :

=SIERREUR(PETITE.VALEUR(nb; LIGNE(INDIRECT('1:' & LIGNES(nb)))); '')

Et bien entendu, pour un tri décroissant, il suffit de remplacer la fonction Petite.Valeur par la fonction Grande.Valeur :

=SIERREUR(GRANDE.VALEUR(nb; LIGNE(INDIRECT('1:'& LIGNES(nb)))); '')