Résoudre des équations à plusieurs inconnues avec Excel

Pour partager cette vidéo sur les réseaux sociaux ou sur un site, voici son url :


Sujets que vous pourriez aussi aimer :


Résoudre des équations avec Excel

Dans cette formation, nous allons construire une petite application capable de résoudre des équations à plusieurs inconnues. Nous proposons d'y parvenir sans le solveur ni code VBA et bases mathématiques. Un peu de bon sens basé sur l'exploitation des connaissances acquises suffira à résoudre le problème.



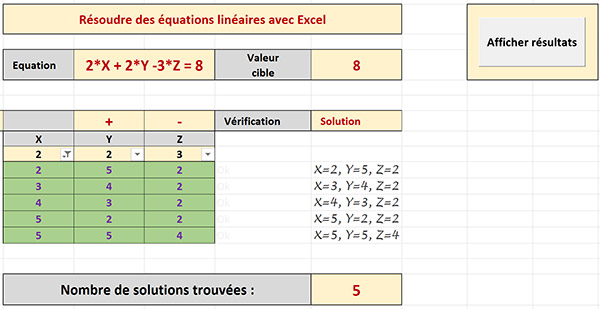
Comme l'illustre la capture ci-dessus de l'application finalisée, un clic sur le bouton Afficher les résultats livre toutes les combinaisons dans la colonne solution. Ce bouton déclenche une macro automatique réalisant une simple action de filtre. Les calculs sont posés dans la feuille Excel en fonction de l'équation à résoudre, inscrite dans la partie supérieure de la feuille. Cette équation elle-même peut être modulée à souhait, en intervenant sur les chiffres et opérateurs en entête du tableau central.

Sources et principe de résolution
Pour la résolution de ce cas, nous proposons de débuter à partir d'un classeur existant, offrant la structure de base, afin de concentrer nos efforts sur les calculs.

• Télécharger le classeur equations-excel.xlsm en cliquant sur son lien,
• L'ouvrir dans Excel et cliquer sur le bouton Activer la modification,

Ce classeur est constitué d'une seule feuille nommée Equation linéaire. L'équation à résoudre comporte au plus 3 inconnues : X, Y et Z, référencées respectivement en cellules C8, D8 et E8. Elles sont associées à un facteur inscrit dans la cellule du dessous, respectivement en C9, D9 et E9. Les opérateurs reliant chacune de ces variables sont désignés en cellules D7 et E7. En fonction de ces paramètres, il s'agit d'atteindre la valeur cible référencée en cellule G4. Dans notre cas, au premier chargement du classeur, il s'agit donc de résoudre l'équation :

3X + 2Y - 3Z = 6

Plusieurs combinaisons sont possibles. La seule contrainte que nous imposons arbitrairement ici est que, les variables ne peuvent pas dépasser le chiffre 5. C'est la raison pour laquelle sont listées en colonnes C, D et E toutes les valeurs possibles. Pour chaque valeur de X inscrite en colonne C, nous faisons varier toutes les valeurs possibles pour Y entre 1 et 5. Et pour chaque valeur de Y, nous faisons varier toutes les valeurs possibles de Z en colonne E, entre 1 et 5. Nous allons donc simuler le principe des boucles de programmation mais sans code VBA Excel. Nous obtenons donc 5³, soit 125 combinaisons possibles. Il s'agit d'extraire celles permettant d'atteindre la valeur cible pour résoudre l'équation.



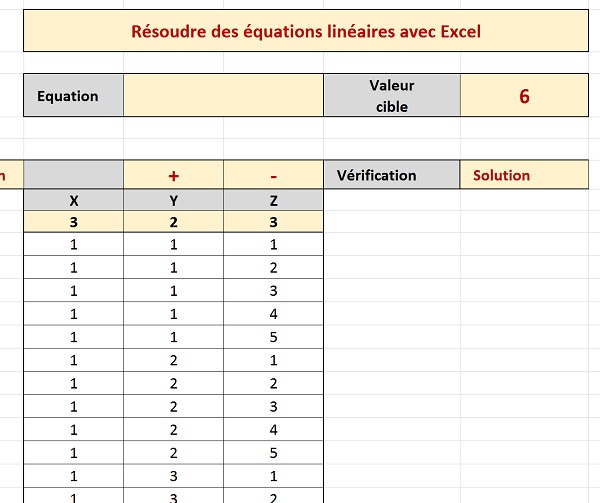
Il s'agira alors d'appliquer une mise en forme conditionnelle sur l'ensemble du tableau pour mettre dynamiquement en valeur les lignes résolvant l'équation. Dès lors un filtre automatique par couleur permettra de masquer toutes les combinaisons n'apportant pas la solution. Ces réglages dépendront du calcul à réaliser dans la colonne Vérification (Colonne F). Ce filtre devra être déclenché automatiquement par le bouton de macro disposé en haut à droite de la feuille.

Reconstruire l'équation par concaténation
Dans un premier temps, nous souhaitons simplement retranscrire explicitement l'équation à résoudre, en cellule D4. Il s'agit donc d'assembler les informations écrites entre les lignes 7 et 9 avec la valeur cible en G4. Comme nous l'avait appris la formation Excel pour assembler des chaînes de caractères, nous devons exploiter le caractère de concaténation pour consolider chaque donnée. Le caractère de concaténation (Et commercial) s'obtient en enfonçant la touche 1, située en haut à gauche du clavier. L'assemblage reste un calcul, donc nous devons débuter l'écriture par le symbole =.

• Sélectionner la cellule D4 et taper le symbole = pour débuter le calcul,
• Sélectionner le premier facteur en cliquant sur la cellule C9,
• Puis, taper le Et commercial (&) et cliquer sur la première inconnue en C8,
• Saisir de nouveau le symbole de concaténation (&) suivi d'un espace entre guillemets (" "),
• Ajouter un autre Et commercial et cliquer sur la cellule du premier opérateur en D7,
• Saisir de nouveau le symbole de concaténation (&) suivi d'un espace entre guillemets (" "),
• Puis, concaténer au deuxième facteur de l'équation en D9 (& D9),
• Associer ce facteur à la deuxième inconnue en D8 (& D8),
• Assembler de nouveau un espace entre guillemets (& " "),
• Puis, concaténer l'ensemble au second opérateur situé en E7,
• Assembler un nouvel espace à la suite (& " "),
• Puis concaténer avec le troisième facteur lui-même concaténé avec la troisième inconnue (& E9 & E8),
• Assembler le tout au symbole = avec des espaces entre guillemets (& " = "),
• Enfin, ajouter un dernier caractère de concaténation et cliquer sur la cellule du résultat à atteindre, soit G4 (& G4),
• Valider le calcul en enfonçant la touche Entrée,

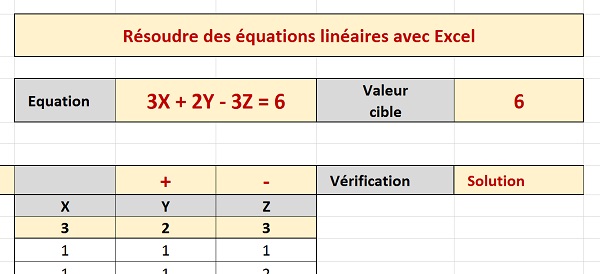
Nous obtenons clairement l'information sur l'équation à résoudre, comme l'illustre la capture ci-dessus. Comme cette équation a été consolidée en fonction des données du problème par concaténation, elle est dynamique. Il suffit de changer un opérateur, un facteur ou encore la valeur cible pour modifier les hypothèses. La formule que nous avons bâtie est la suivante :

=C9 & C8 & " " & D7 & " " & D9 & D8 & " " & E7 & " " & E9 & E8 & " = " & G4

• En G4, remplacer la valeur cible par le chiffre 8,
• En D7, remplacer l'opérateur + par l'opérateur -,
• Inversement en E7, remplacer l'opérateur - par l'opérateur +,
• En D9, modifier la valeur du deuxième facteur en tapant le chiffre 4,

Au fur et à mesure des modifications, l'équation à résoudre s'est mise à jour en cellule D4. Désormais, nous devons trouver les inconnues permettant de solutionner l'équation suivante :

3X - 4Y + 3Z = 8

Remarque : Pour afficher les symboles - et + en D7 et E7, nous avons préfixé la saisie d'une apostrophe. Cette astuce indique à Excel de ne pas interpréter l'information qui suit et de la conserver telle quelle. C'est ce qu'illustre la capture ci-dessous. Ce caractère apparaît dans la barre de formule mais pas dans la cellule. Sans cette apostrophe, Excel aurait interprété un calcul générant une erreur.

Nous l'avions d'ailleurs exploitée pour conserver les zéros en préfixes des codes postaux et numéros de téléphone même si dans ce cas, il existe des formats de cellules adaptés.



Calcul récursif pour vérifier l'équation
Dans la colonne Vérification (F), nous souhaitons inscrire un repère textuel lorsque la combinaison des valeurs conduit au résultat à atteindre. Arbitrairement, nous inscrirons le texte Ok. Dès lors nous exploiterons cette information pour déclencher un format conditionnel mettant en valeur l'ensemble de la ligne solutionnant l'équation. Ce format dynamique étant lui-même relié à un calcul, les mises en valeur varieront ainsi automatiquement, selon l'équation à résoudre. Mais c'est en réalité quatre équations que nous devons tester, selon les opérateurs employés. Les cas sont les suivants : + et +, + et -, - et + puis - et -. Nous devons imbriquer des fonctions Excel Si. Et comme les critères à vérifier sont multiples, nous devons exploiter la fonction Excel Et afin de les énumérer. Voici le raisonnement à poser :

Si les deux opérateurs valent le symbole + et que l'équation ainsi construite vaut la valeur cible :
SI(ET(D7="+"; E7="+"; C10*C9+D10*D9+E10*E9=G4); "Ok"

Dans la fonction ET, nous énumérons trois critères. Ils doivent être vérifiés ensemble. Si l'un d'entre eux ne l'est pas, le critère global est considéré comme non vérifié. Dans le cas contraire, nous pouvons inscrire le repère textuel de succès (Ok), indiquant que l'équation ainsi reconstruite (Facteurs, opérateurs, valeurs, valeur cible) est solutionnée.

Sinon, si les deux opérateurs sont respectivement le + et le - et que l'équation ainsi reconstruite atteint la valeur cible :
SI(ET(D7="+"; E7="-"; C10*C9+D10*D9-E10*E9=G4); "Ok"

Sinon, si les deux opérateurs sont respectivement le - et le + et que l'équation ainsi reconstruite atteint la valeur cible :
SI(ET(D7="-"; E7="+"; C10*C9-D10*D9+E10*E9=G4); "Ok"

Sinon, si l'équation exploitant les opérateurs - seulement rejoint le résultat :
SI(C10*C9-D10*D9-E10*E9=G4; "Ok"

En imbriquant ainsi les fonctions conditionnelles, nous serons capables de vérifier les quatre équations possibles pour offrir une certaine modularité à l'utilisateur, dans la construction et la résolution de ces équations à trois inconnues.

Dans le cas restant (le dernier sinon), nous en déduirons qu'aucun des critères précédents n'a été vérifié et en conséquence, que la solution n'a pas été trouvée. Dans ce cas, nous laisserons la cellule vide. Pour que la formule finale puisse être répliquée sur l'ensemble de la colonne Vérification, nous devons exploiter les références absolues d'Excel. Comme nous désignons des cellules qui ne doivent pas bouger lorsque nous répliquons le calcul sur les lignes du dessous, nous devons les figer grâce à la touche F4 du clavier. Les références des cellules concernées seront alors encadrées de dollars ($). Ces cellules toujours situées sur la même ligne sont respectivement : C9, D9, E9, D7, E7 et G4.

• Sélectionner la première cellule du calcul, soit F10,
• Taper le symbole = pour débuter la formule,
• En imbriquant les calculs énumérés juste au-dessus (séparés par des points-virgules) et en figeant les cellules listées précédemment, reconstruire le calcul final :

=SI(ET($D$7="+"; $E$7="+"; C10*$C$9+D10*$D$9+E10*$E$9=$G$4); "Ok"; SI(ET($D$7="+"; $E$7="-"; C10*$C$9+D10*$D$9-E10*$E$9=$G$4); "Ok"; SI(ET($D$7="-"; $E$7="+"; C10*$C$9-D10*$D$9+E10*$E$9=$G$4); "Ok"; SI(C10*$C$9-D10*$D$9-E10*$E$9=$G$4; "Ok";""))))

• Valider la formule par le raccourci CTRL + Entrée pour conserver la cellule active,
• Double cliquer sur la poignée de la cellule F10 pour répliquer le calcul sur la hauteur du tableau,

Quelques inscriptions Ok apparaissent subtilement dans certaines cellules du fait de la couleur de mise en forme préréglée sur un gris très clair. Elles attestent de la validation de l'équation en considérant les valeurs de la ligne en cours, en lieu et place des inconnues. Pour figer une cellule dans le calcul, vous pouvez saisir les $ directement au clavier ou encore, enfoncer la touche F4 après avoir pris soin de placer le point d'insertion sur les références de la cellule.



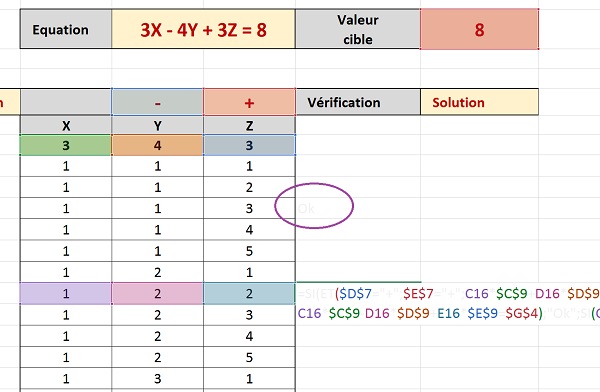
Comme l'illustre la capture ci-dessus, la cellule F12 indique que les valeurs de la ligne conduisent au résultat pour l'équation : 3X - 4Y + 3Z = 8. En effet : 3*1 - 4*1 + 3*3 = 3 - 4 + 9 = 8. Notre calcul principal semble donc fonctionnel puisque d'autres solutions sont suggérées.

Afficher les solutions de l'équation
Avant d'offrir une mise en forme dynamique sans équivoque sur l'ensemble des lignes offrant une solution, nous souhaitons afficher explicitement les valeurs proposées respectivement pour chacune des inconnues. Donc dans la colonne G, nous proposons de concaténer chacune des valeurs de la ligne avec son inconnue. Une fois encore, la concaténation consiste en un calcul faisant intervenir des cellules à figer. Il s'agit des inconnues. Les références absolues entrent à nouveau en jeu. L'assemblage ne doit être réalisé que si la solution a été trouvée. Une fonction Si doit donc tester que la valeur inscrite en colonne F est bien le texte Ok.

• Sélectionner la cellule G10 et taper le symbole = pour débuter le calcul,
• Taper le nom de la fonction conditionnelle suivi d'une parenthèse ouvrante, soit SI(,
• Sélectionner la première cellule à tester, soit F10,
• Saisir le symbole = suivi du texte Ok entre guillemets pour le critère à vérifier, soit ="Ok",
• Taper un point-virgule (;) pour passer à l'argument Alors de la fonction Si,
• Sélectionner la première inconnue, soit la cellule C8 et enfoncer la touche F4 pour la figer,
• La concaténer au symbole = et à sa valeur correspondante sur la ligne, soit & "=" & C10,
• Ajouter la concaténation d'une virgule suivie d'un espace, soit & ", ",
• Assembler alors la deuxième inconnue en la figeant, soit & $D$8,
• La concaténer au symbole = et à sa valeur correspondante sur la ligne, soit & "=" & D10,
• Ajouter la concaténation d'une virgule suivie d'un espace, soit & ", ",
• Assembler alors la troisième inconnue en la figeant, soit & $E$8,
• La concaténer au symbole = et à sa valeur correspondante sur la ligne, soit & "=" & E10,
• Taper un point-virgule (;) pour passer dans la branche Sinon de la fonction Si,
• Saisir deux guillemets pour garder une cellule vide lorsque le critère n'est pas vérifié,
• Fermer la parenthèse de la fonction Si et valider le calcul par CTRL + Entrée,
• Double cliquer sur la poignée de la cellule pour répliquer le calcul sur tout le tableau,

Le calcul que nous avons bâti est le suivant :
=SI(F10="Ok";$C$8& "=" & C10 & ", " & $D$8 & "=" & D10 & ", " & $E$8 & "=" & E10;"")



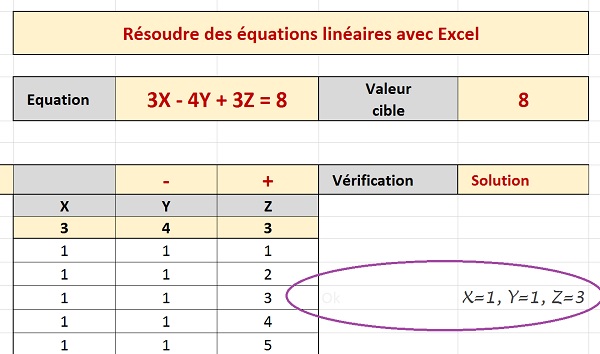
Désormais, les valeurs des inconnues s'affichent en regard des lignes correspondant à des combinaisons solutionnant l'équation, selon le test réalisé dans la colonne précédente. Comme tous les calculs sont dynamiques, si nous modifions certains paramètres de l'équation, les solutions se mettent à jour en proposant les nouvelles valeurs associées aux inconnues.

Mise en valeur des solutions de l'équation
Comme le tableau est assez long, nous souhaitons lui associer une mise en forme conditionnelle capable de faire ressortir toute la ligne en couleur, lorsque la combinaison résout l'équation. Une mise en forme conditionnelle est un format dynamique qui réagit en fonction du contenu des cellules. Les couleurs s'adapteront automatiquement aux modifications des données du problème. Cette mise en forme se réalise donc selon des conditions ou plutôt un critère à vérifier. S'il est inscrit le texte Ok dans la colonne F, l'ensemble de la ligne doit être mise en valeur. La formation Excel pour créer des synoptiques nous avait appris à faire réagir l'aspect de plages en fonction de critères posés sur d'autres cellules. Pour placer un format dynamique, nous devons commencer par sélectionner les cellules concernées.

• Cliquer sur la cellule C10 pour sélectionner la première référence concernée,
• Faire défiler la feuille vers le bas jusqu'à visualiser la fin du tableau,
• Avec la touche MAJ enfoncée (Shift), cliquer la dernière cellule concernée, soit E134,
• Cliquer alors sur le bouton Mise en forme conditionnelle sur la droite du ruban Accueil,
• Dans la liste, choisir Nouvelle règle,
• Dans la liste des types de règles de la boîte de dialogue, sélectionner la dernière (Utiliser une formule pour déterminer pour quelles cellules le format sera appliqué),
• Cliquer dans la zone de saisie juste en dessous pour l'activer,
• Sélectionner la première cellule de la colonne vérification, soit F10,
• Enfoncer deux fois de suite la touche F4 pour ne conserver qu'un seul dollar, celui devant l'indice de colonne,

En effet, le critère doit être vérifié pour toutes les lignes du tableau. Donc la cellule doit se déplacer vers le bas en suivant le sens de la vérification. C'est pourquoi nous ôtons le dollar situé devant l'indice de ligne. En revanche, pour une même ligne, le critère ne peut être vérifié qu'en colonne F. La cellule ne doit donc pas se déplacer sur la largeur de la ligne. C'est la raison pour laquelle nous conservons la colonne figée.

• Taper le symbole = suivi du texte Ok entre guillemets, soit au final =$F10="Ok",

Lorsque ce critère est vérifié sur une ligne, l'ensemble des cellules doit réagir. Nous devons donc lui associer un format.

• Cliquer sur le bouton Format situé en bas de la boîte de dialogue,
• Dans la boîte de dialogue qui suit, activer l'onglet Remplissage,
• Cliquer sur le bouton Motifs et textures,
• Créer alors un dégradé de couleurs du blanc vers un jaune orangé par exemple,
• Valider par Ok et cliquer sur l'onglet Police de la boîte de dialogue,
• Choisir le style gras,
• Puis sélectionner une couleur de police rouge foncé à l'aide de la liste déroulante,
• Valider ces réglages par le bouton Ok,
• Puis valider la première boîte de dialogue,

De retour sur la feuille, vous constatez que toutes les lignes offrant une solution à l'équation sont mises en valeur selon les réglages que nous venons de paramétrer. Si nous modifions les paramètres de l'équation, les lignes offrant la bonne combinaison changent et les couleurs les accompagnent.



Filtrer les solutions par couleur
Comme nous l'avait appris la formation Excel pour manipuler les bases de données, les filtres automatiques peuvent isoler les lignes mises en valeur par un format conditionnel. Ainsi nous proposerons de regrouper toutes les combinaisons offrant une solution à l'équation.

• Sélectionner la plage de cellules C9 à E9, soit les entêtes du tableau,
• Tout à fait à droite du ruban Accueil, cliquer sur le bouton Trier et filtrer,
• Dans la liste, choisir Filtrer,

Ainsi des petites flèches de filtres automatiques apparaissent en haut de chaque colonne du tableau.

• Cliquer sur l'une de ces flèches de filtre,
• Dans la liste, pointer sur Filtrer par couleur,
• Puis, dans le sous-menu, cliquer sur le visuel du dégradé correspondant au format dynamique,

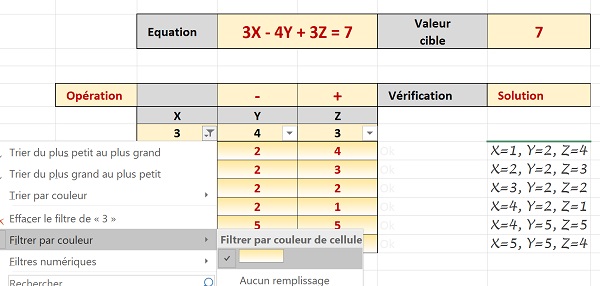
Ainsi toutes les lignes mises en forme conditionnellement, donc solutionnant l'équation, sont regroupées et l'application commence à prendre forme. En quelques clics désormais, il est effectivement très simple d'obtenir la synthèse de toutes les combinaisons satisfaisant l'équation. Mais nous allons encore améliorer l'ergonomie pour qu'un seul clic soit nécessaire à la synthèse des résultats.

Avant cela, nous souhaitons parfaire la pertinence des résultats offerts. En cellule G137, nous devons afficher le nombre de combinaisons trouvées pour résoudre l'équation. Nous pourrions exploiter la fonction Excel NbVal qui comptabilise le nombre de cellules non vides sur une plage définie. Mais comme nous l'avait appris la formation Excel sur le calcul des données filtrées, la formule =NBVAL(G10:G134) retournerait la valeur 125, soit l'ensemble des cellules de la colonne. Les fonctions classiques considèrent les cellules filtrées dans le calcul bien qu'elles soient masquées. Pour les exclure, nous avions appris à exploiter la fonction Sous.Total qui permet de réaliser de nombreux calcule selon un paramètre à définir.

• En cellule G137, taper le symbole = pour débuter le calcul,
• Saisir le nom de la fonction de synthèse suivi d'une parenthèse ouvrante, soit sous.total(,
• Taper le chiffre 3 pour désigner la fonction NbVal dans le calcul,
• Taper un point-virgule pour passer à l'argument suivant,
• Saisir alors la plage de cellules G10:G134 pour désigner la colonne complète,
• Fermer la parenthèse de la fonction et valider le calcul par la touche Entrée,

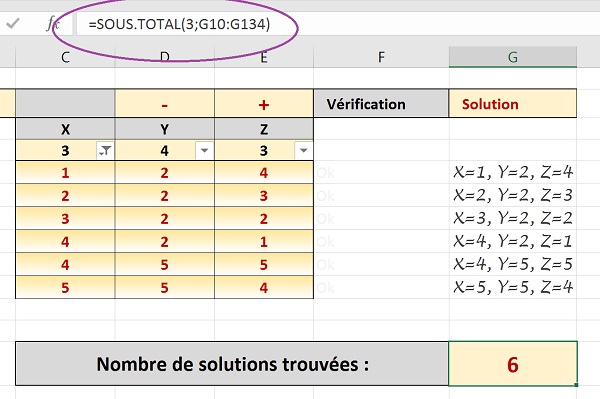
Cette fois le résultat est cohérent avec les données filtrées et dynamiques de surcroît. L'application indique à l'utilisateur que six combinaisons d'inconnues fournissent le résultat de l'équation.

• Cliquer sur la flèche du filtre actif en haut du tableau,
• Dans la liste, choisir Effacer le filtre,
• En G4, passer la valeur cible de 7 à 12,
• Cliquer de nouveau sur la flèche du filtre automatique,
• Puis choisir, comme précédemment, de filtrer sur la couleur du format dynamique.

Nous obtenons toutes les confirmations sur les hypothèses que nous avancions. L'application est parfaitement dynamique. Tout d'abord les calculs ne proposent plus que 3 combinaisons validant l'équation. Les couleurs se sont automatiquement adaptées. Le filtre automatique a permis de regrouper les solutions. Et le calcul de synthèse indique clairement que seules 3 combinaisons fonctionnent pour atteindre la nouvelle valeur cible.

Protéger les cellules de l'application
Pour protéger l'application, seules les cellules permettant de modifier l'équation doivent autoriser la saisie. Il s'agit des facteurs en cellules C9, D9 et E9 ainsi que des opérateurs en cellules D7 et E7 et de la valeur cible en G4. Comme nous l'avions appris dans la formation pour monter une facturation et la protéger à l'issue, nous devons d'abord déverrouiller ces cellules et ensuite protéger la feuille. Ainsi, toutes les cellules non déverrouillées ne pourront plus être modifiées par mégarde.

• A l'aide de la touche CTRL, sélectionner ensemble les cellules C9, D9, E9, D7, E7 et G4,
• Puis réaliser un clic droit sur l'une des cellules sélectionnées,
• Dans le menu contextuel, choisir Format de cellule,
• Dans la boîte de dialogue qui suit, activer l'onglet Protection,
• Décocher la case verrouillée et cliquer sur Ok pour valider,
• Cliquer ensuite sur la flèche du filtre en cours et choisir Effacer le filtre,
• Cliquer sur l'onglet Révision en haut de la fenêtre Excel pour activer son ruban,
• Sur la droite du ruban, cliquer sur le bouton Protéger la feuille,
• Dans la boîte de dialogue qui suit, cliquer sur Ok pour activer la protection sans mot de passe,
• En G4, changer la valeur cible 12 en 15,
• En cellule F10, taper le symbole = pour simuler le début d'un nouveau calcul,

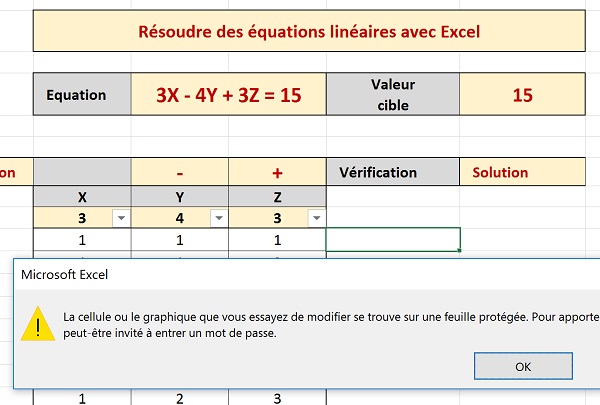
Comme vous le constatez, puisque cette cellule portant un calcul n'a pas été déverrouillée avant la protection de la feuille, elle est protégée contre toute modification inopportune. En revanche, nous avons pu changer la valeur cible de l'équation, comme nous aurions pu le faire pour les opérateurs et facteurs.

Automatiser la résolution de l'équation
Pour parfaire l'ergonomie de notre application de résolution des équations à 3 inconnues, nous souhaitons livrer les résultats regroupés et synthétisés par simple clic sur le bouton. Un clic sur le bouton doit exécuter une macro qui enclenche le filtre par couleur sur le tableau des valeurs d'inconnues. Cependant une macro au même titre qu'un utilisateur se heurtera à la protection active sur la feuille. Nous devons donc enregistrer une macro ôtant la protection de la feuille, enclenchant le filtre par couleur et réactivant la protection. Si l'onglet Développeur n'est pas proposé en haut de votre fenêtre Excel, vous pouvez vous référer à la formation pour débuter la programmation VBA Excel.

• Cliquer sur l'onglet Développeur en haut de la fenêtre Excel pour activer son ruban,
• Dans la section Code tout à fait à gauche, cliquer sur le bouton Enregistrer une macro,
• Dans la boîte de dialogue qui suit, taper le nom resultats sans accents,
• Valider par Ok pour débuter l'enregistrement,
• Cliquer alors sur l'onglet Révision pour activer son ruban,
• Cliquer ensuite sur le bouton Ôter la protection de la feuille,
• Cliquer sur l'une des flèches de filtre automatique en haut du tableau,
• Choisir de filtrer sur la couleur de la mise en forme conditionnelle,
• Dans le ruban Révision, cliquer sur le bouton Protéger la feuille et valider par Ok,
• Cliquer de nouveau sur l'onglet Développeur pour revenir sur son ruban,
• Dans la section Code tout à fait à gauche, cliquer sur le bouton Arrêter l'enregistrement,

La macro existe, traduite en code VBA, mais elle n'est pas encore matérialisée. Pour qu'elle reproduise les actions que nous avons simulées, nous devons l'attacher au bouton présent sur la feuille. Mais pour cela, nous devons préalablement ôter de nouveau la protection de feuille.

• Dans l'onglet Révision, cliquer sur le bouton Ôter la protection de la feuille,
• Sur la feuille, cliquer droit sur le bouton Afficher les résultats,
• Dans le menu contextuel, choisir Affecter une macro,
• Dans la boîte de dialogue, sélectionner la macro resultats et valider par Ok,
• Dans le ruban Révision, cliquer de nouveau sur le bouton Protéger la feuille,

Il est temps de tester l'ergonomie de notre application de résolution d'équations.

• En cellule G4,taper le nombre 19 pour la nouvelle valeur cible à atteindre,
• En D7 et E7, taper le symbole +,
• En C9, D9 et E9, saisir les facteurs respectifs 2, 1 et 1,
• Puis, cliquer sur le bouton Afficher les résultats,

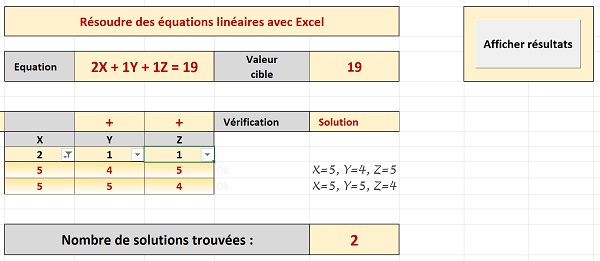
Comme vous le constatez et comme l'illustre la capture ci-dessus, pour la nouvelle équation ainsi construite : 2X + 1Y + 1Z = 19, l'application ne propose plus que deux solutions pour la combinaison des trois inconnues conduisant au résultat. La synthèse se construit instantanément au clic sur le bouton. Nous avons réussi à bâtir une application pour résoudre les équations à trois inconnues sans code VBA ni solveur.