Trouver les lignes des valeurs situées dans la fourchette

Pour partager cette vidéo sur les réseaux sociaux ou sur un site, voici son url :


Sujets que vous pourriez aussi aimer :


Compter les lignes répondant aux critères

L'objectif de cette nouvelle astuce Excel est de déterminer le nombre de lignes qui portent des valeurs inférieures à un nombre spécifié et répétées au moins autant de fois que demandé.



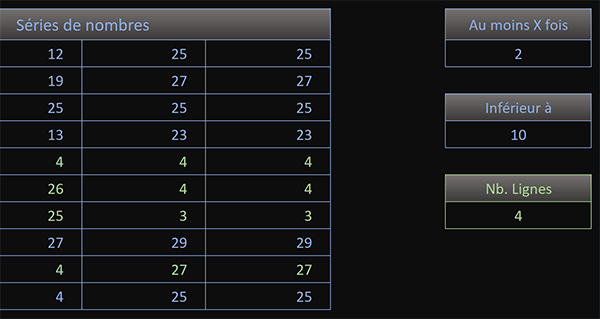
Dans l'exemple illustré par la capture, nous travaillons sur un tableau rempli de nombres. Sur la droite et dans une première case, l'utilisateur indique la quantité minimum de répétitions à observer pour les données acceptant la contrainte mentionnée dans une deuxième case juste en-dessous. Ces valeurs répétées ne doivent pas dépasser le score inscrit. Et dans une dernière case, nous devons comptabiliser les lignes de ce tableau recoupant ces contraintes.

Classeur source
Pour la mise en place de cette astuce, nous proposons de récupérer un classeur Excel déjà rempli de ces informations à manipuler.

• Télécharger le classeur ligne-recherches.xlsx en cliquant sur ce lien,
• Double cliquer sur le fichier réceptionné pour l'ouvrir dans Excel,
• Puis, cliquer sur le bouton Activer la modification du bandeau de sécurité,

Les deux contraintes sont donc à inscrire en cellules respectives G4 et G7. Le nombre de lignes répondant à ces critères doit être calculé en cellule G10. Si vous déployez la zone Nom en haut à gauche de la feuille Excel, vous notez que le tableau de données est reconnu sous l'intitulé Series.

Dénombrer les lignes concordantes
C'est un raisonnement matriciel semblable à celui de l'astuce du volet précédent qui permet de résoudre le cas. Nous devons de nouveau imbriquer les fonctions ProduitMat, Transpose et Colonne dans la fonction Somme. Les critères issus du tableau de bord doivent être posés sur les matrices que nous allons ainsi composer.

• Cliquer sur la cellule G10 pour la sélectionner,
• Taper le symbole égal (=) pour initier la formule matricielle,
• Inscrire la fonction d'addition suivie d'une parenthèse, soit : Somme(,
• Ouvrir une nouvelle parenthèse pour la factorisation à entreprendre,
• Taper la fonction pour multiplier deux matrices, suivie d'une parenthèse, soit : ProduitMat(,
• Ouvrir une nouvelle parenthèse pour entreprendre une factorisation imbriquée,
• Désigner le tableau des nombres par son nom, soit : Series,
• Taper le symbole inférieur (<) pour annoncer le critère à honorer,
• Puis, cliquer sur la cellule G7 pour désigner la contrainte dynamique à respecter,
• Fermer la parenthèse de la factorisation,
• Puis, multiplier cette matrice conditionnelle par le chiffre 1, soit : *1,

Prenons le temps d'expliquer ce premier calcul (series<G7)*1 : Sur la plage des nombres nommée Series, le raisonnement matriciel inscrit des indicateurs booléens (True ou False) sur les positions des cases du tableau, en fonction des concordances ou non concordances avec le critère. La multiplication par 1 transforme ces indicateurs en chiffres (1 ou 0). Bref, nous connaissons désormais les emplacements des cellules pour lesquelles le second critère mentionné en cellule G7 est respecté.

Nous devons maintenant recouper cette matrice conditionnelle ainsi construite avec une autre matrice. L'ensemble ainsi recoupé devra porter sa condition sur le premier critère mentionné en cellule G4.

• Taper un point-virgule (;) pour passer dans l'argument de la seconde matrice de ProduitMat,
• Inscrire la fonction pour retourner un tableau, suivie d'une parenthèse, soit : Transpose(,
• Inscrire la fonction indiquant l'indice de colonne, suivie d'une parenthèse, soit : Colonne(,

Dans ce raisonnement matriciel, ce sont tous les indices de colonnes du tableau qui vont être retournés, à condition que nous le passions bien en paramètre de la fonction Colonne.

• Désigner le tableau des nombres par son intitulé, soit : Series,
• Puis, fermer la parenthèse de la fonction Colonne,
• Enfoncer la touche de l'accent circonflexe puis inscrire le chiffre zéro, soit : ^0,

La fonction Colonne renvoie un tableau des positions de 4 colonnes {2,3,4,5}. En élevant ce tableau à la puissance zéro (^0), nous le transformons en un tableau rempli de chiffres 1 de la forme 4 colonnes x 1 ligne : {1,1,1,1}. Grâce à la fonction Transpose, nous le retournons et le transformons sous la forme 1 colonne x 4 lignes.

• Fermer la parenthèse de la fonction Transpose,
• Puis, fermer la parenthèse de la fonction ProduitMat,
• Taper le symbole supérieur suivi du symbole égal, soit : >=,
• Puis, désigner la première contrainte à honorer en cliquant sur sa cellule G4,

A ce stade, la fonction ProduitMat qui croise les deux matrices ainsi confectionnées, retourne un tableau de 10 lignes où les positions repérées sont cumulées, par exemple : {2; 0; 0; 3; 0; 0; 0; 1; 0; 0}. Grâce à l'expression logique >= G4 pour honorer la première contrainte, nous obtenons un tableau des lignes répondant favorablement aux deux conditions, sanctionnées par des indicateurs booléens. Nous devons une fois encore transformer ces derniers en chiffres.

• Fermer la parenthèse de la factorisation,
• Réaliser la conversion des booléens, soit : *1,
• Fermer la parenthèse de la fonction Somme,
• Enfin, valider nécessairement la formule matricielle par le raccourci CTRL + MAJ + Entrée,

Le résultat tombe et confirme le nombre de lignes répondant aux deux conditions. Bien sûr, si vous modifiez ces contraintes, les calculs s'actualisent automatiquement.



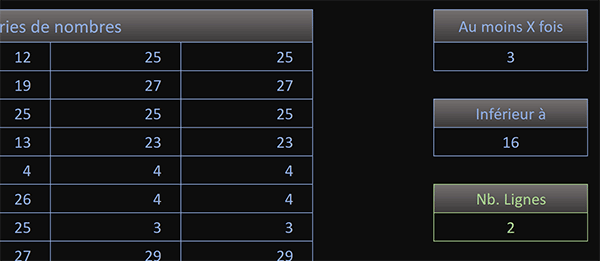
Par exemple, deux lignes seulement portent au moins trois nombres inférieurs à 16. La syntaxe complète de la formule matricielle que nous avons construite est la suivante :

{=SOMME((PRODUITMAT((series<G7)*1; TRANSPOSE(COLONNE(series)^0))>=G4)*1)}

Repérer les lignes concordantes
Même si ce résultat calculé est très simple à confirmer, il est encore plus judicieux de faire ressortir explicitement les lignes concernées. Et pour cela, nous proposons de bâtir une règle de mise en forme conditionnelle.

• Sélectionner tous les nombres du tableau, soit la plage de cellules B4:E13,
• Dans la section Styles du ruban Accueil, cliquer sur le bouton Mise en forme conditionnelle,
• En bas de la liste des propositions, choisir l'option Nouvelle règle,
• Dans la boîte de dialogue qui suit, sélectionner la catégorie Utiliser une formule pour ...,
• Puis, cliquer dans la zone de saisie du dessous pour l'activer,
• Taper le symbole égal (=) pour initier la syntaxe de la règle de mise en forme conditionnelle,
• Inscrire la fonction de dénombrement conditionnel suivie d'une parenthèse, soit : Nb.Si(,
• Désigner la première ligne du tableau, soit la plage de cellules $B$4:$E$4,
• Enfoncer deux fois la touche F4 du clavier, ce qui donne : $B4:$E4,

Comme vous le savez, l'analyse d'une mise en forme conditionnelle est chronologique. Nous débutons donc l'étude à partir de la première ligne pour qu'elles soient toutes passées en revue tour à tour. C'est la raison pour laquelle nous libérons la plage en ligne. Sur chaque ligne, nous devons vérifier les deux conditions avec une seule formule.

• Taper un point-virgule (;) pour passer dans l'argument du critère de la fonction Nb.Si,
• Construire alors la syntaxe suivante : "<" & $G$7,

Nous cherchons donc à compter le nombre de fois que des valeurs sont inférieures à la deuxième contrainte énoncée et ce, pour chaque ligne.

• Fermer la parenthèse de la fonction Nb.Si,
• Puis, ajouter le critère recoupé suivant : >=$G$4,

Cette quantité calculée par la fonction Nb.Si doit dans le même temps être au moins égale à la première condition formulée par l'utilisateur. Lorsque ces conditions croisées sont vérifiées, nous devons faire ressortir les lignes concernées par des attributs de format explicitement différents.

• Cliquer sur le bouton Format en bas de la boîte de dialogue,
• Dans la boîte de dialogue qui suit, activer l'onglet Police,
• Avec la deuxième liste déroulante, choisir un vert assez clair pour la couleur du texte,
• Valider ces attributs de format avec le bouton Ok,
• De retour sur la première boîte de dialogue, valider la création de la règle par Ok,

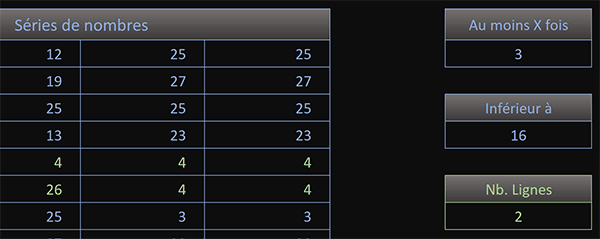
Instantanément, ce repérage visuel dynamique vient parfaitement recouper le résultat offert par la formule matricielle.