Apprendre à maîtriser la fonction Excel Sequence

Pour partager cette vidéo sur les réseaux sociaux ou sur un site, voici son url :


Sujets que vous pourriez aussi aimer :


Présentation de la fonction Sequence

Dans ce premier volet, pour débuter simplement les découvertes au sujet des possibilités offertes par la fonction Excel Sequence, nous allons apprendre à créer des suites numériques logiques et maîtrisées.



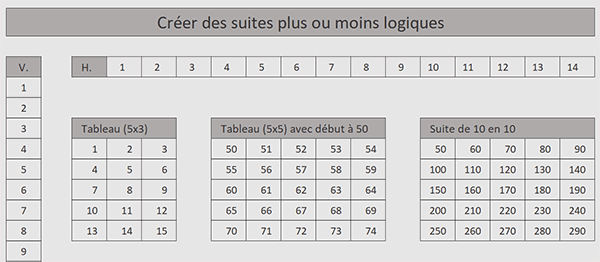
Sur l'exemple illustré par la capture, nous créons automatiquement différents types de suites logiques. La première est verticale. Elle est incrémentée normalement sur dix unités. La deuxième est horizontale. Elle est incrémentée normalement sur quatorze unités. La troisième remplit un tableau de cinq lignes et de trois colonnes. La quatrième crée un tableau de nombres de cinq lignes et cinq colonnes, mais elle débute son énumération à partir du nombre cinquante. La dernière débute aussi à partir de cinquante mais incrémente les nombres suivants de dix unités, toujours dans un tableau de cinq lignes et de cinq colonnes.

Classeur Excel à télécharger
Cette étude peut se faire depuis un classeur vierge. Cependant, nous suggérons de récupérer un classeur offrant une structure propice à la construction de ces listes.

• Télécharger le classeur decouvrir-fonction-sequence.xlsx en cliquant sur ce lien,
• Double cliquer sur le fichier réceptionné pour l'ouvrir dans Excel,
• Puis, cliquer sur le bouton Activer la modification du bandeau de sécurité,

Nous découvrons une feuille semblable à celle de la présentation, mais toutes les grilles sont fort naturellement vides pour l'instant.

Les arguments de la fonction Sequence
La fonction Sequence peut admettre jusqu'à quatre paramètres. Mais seul le premier est obligatoire. Voici sa signature : =sequence(lignes; [colonnes]; [début]; [pas]). Les arguments entre crochets sont facultatifs.

Le premier argument est le seul à être obligatoire, nous l'avons dit. Il définit le nombre de lignes sur lesquelles la suite logique doit être créée. Le deuxième définit le nombre de colonnes pour créer un tableau de séries logiques. Le troisième définit le point ou numéro de départ. Le dernier permet de spécifier le pas de l'incrémentation.

Nous le verrons au fil de l'apprentissage, imbriquée dans d'autres fonctions, elle peut aussi s'avérer d'une aide précieuse dans des contextes variés. Il s'agit bien d'une fonction matricielle puisque dans tous les cas, elle répond par un tableau de données.

Suite logique verticale de 10 unités
En colonne B et à partir de la ligne 6, nous devons tout d'abord créer une suite logique, naturellement incrémentée et débutant à partir du chiffre 1.

• Cliquer sur la cellule B6 pour sélectionner la première case de la première série,
• Taper le symbole égal (=) pour initier la syntaxe de la formule,
• Inscrire la fonction de suites numériques, suivie d'une parenthèse, soit : Sequence(,
• Taper le nombre 10 pour créer une série logique de 10 numéros,
• Fermer la parenthèse de la fonction Sequence,
• Puis, valider la formule par la touche Entrée du clavier,

Comme vous pouvez le voir, cette fonction matricielle répand automatiquement ses résultats sur les lignes du dessous pour créer une suite logique verticale de numéros, tous incrémentés d'une unité par rapport aux précédents.

Suite logique horizontale de 14 unités
Pour créer la série logique, naturellement incrémentée en ligne 5, nous devons utiliser les deux premiers arguments de la fonction Sequence. Nous devons lui indiquer qu'elle doit se répandre seulement sur une ligne et dans le même temps, sur quatorze colonnes.

• Cliquer sur la cellule E5 pour désigner le point de départ de la suite horizontale,
• Taper le symbole égal (=) pour débuter la construction de la formule,
• Inscrire la fonction de suites numériques, suivie d'une parenthèse, soit : Sequence(,
• Taper le chiffre 1 pour construire une suite sur une ligne,
• Taper un point-virgule (;) pour passer dans l'argument du nombre de colonnes,
• Inscrire le nombre 14 pour créer une suite horizontale de quatorze unités,
• Fermer la parenthèse de la fonction Sequence,
• Puis, valider la formule par la touche Entrée du clavier,

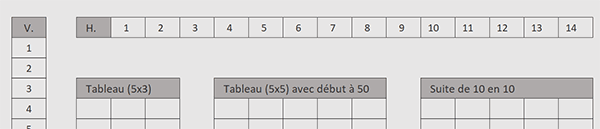
Grâce aux deux premiers paramètres de la fonction Sequence, nous parvenons effectivement à créer une suite logique horizontale, naturellement incrémentée sur le nombre de colonnes défini en deuxième argument.

Suite dans un tableau de 5 lignes et 3 colonnes
Nous allons le découvrir maintenant, lorsque nous paramétrons un nombre de lignes et un nombre de colonnes, tous deux supérieurs à l'unité, l'incrémentation débute naturellement sur les colonnes pour se poursuivre sur les lignes. En d'autres termes, elle est prioritaire à l'horizontale et complémentaire à la verticale.

• Cliquer sur la cellule D9 pour désigner le point de départ de la suite à deux dimensions,
• Taper le symbole égal (=) pour initier la syntaxe de la formule,
• Inscrire la fonction de suites numériques, suivie d'une parenthèse, soit : Sequence(,
• Taper le chiffre 5 pour les cinq lignes à remplir,
• Taper un point-virgule (;) pour passer dans l'argument du nombre de colonnes,
• Inscrire le chiffre 3 pour les trois colonnes à compléter,
• Fermer la parenthèse de la fonction Sequence et valider par la touche Entrée du clavier,

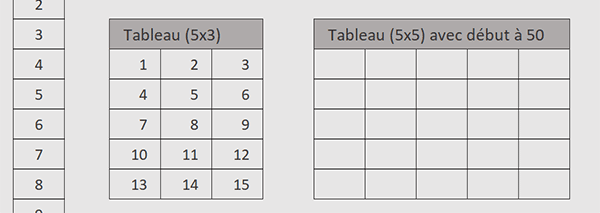
Nous obtenons bien la suite bidirectionnelle, incrémentée sur 15 unités (5 lignes X 3 colonnes), qui progresse prioritairement à l'horizontale et qui poursuit sur les lignes du dessous à chaque butée.

Suite de 5 lignes et 5 colonnes débutant à 50
Nous proposons maintenant d'aller encore plus loin. Pour créer une suite logique bidirectionnelle mais débutant son incrémentation à partir d'une valeur précise, différente du chiffre 1, nous devons régler le troisième paramètre facultatif de la fonction Sequence.

• Cliquer sur la cellule H9 pour désigner le point de départ de l'avant dernier tableau,
• Taper le symbole égal (=) pour démarrer la construction de la formule,
• Inscrire la fonction de suites numériques, suivie d'une parenthèse, soit : Sequence(,
• Taper le chiffre 5 pour construire une suite de cinq lignes,
• Taper un point-virgule (;) pour passer dans l'argument du nombre de colonnes,
• Taper le chiffre 5 pour étendre cette suite sur cinq colonnes,
• Taper un point-virgule (;) pour passer dans l'argument du point de départ de cette suite,
• Inscrire le nombre 50 pour que la série débute son incrémentation à partir de cet indice,
• Fermer la parenthèse de la fonction Sequence et valider la formule par la touche Entrée,

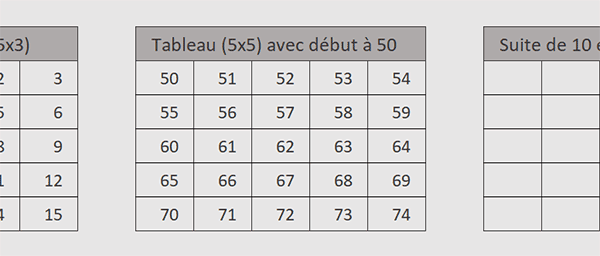
Nous obtenons bien une suite logique bidirectionnelle, naturellement incrémentée sur 25 unités (5 lignes X 5 colonnes) mais qui débute cette fois à partir du nombre 50.

Changer le pas de l'incrémentation
Pour finir, nous souhaitons remplir un tableau similaire à celui que nous venons d'implémenter. Il est fait de 5 lignes et de 5 colonnes. La série doit aussi commencer à partir du nombre 50. Mais cette fois, elle doit progresser de 10 unités à chaque incrémentation. Il est donc question d'influer en plus sur le pas, en quatrième paramètre de la fonction Sequence.

• Cliquer sur la cellule N9 pour désigner le point de départ du dernier tableau,
• Taper le symbole égal (=) pour débuter la construction de la formule,
• Inscrire la fonction de séries logiques, suivie d'une parenthèse, soit : Sequence(,
• Inscrire le chiffre 5 pour construire une suite logique sur cinq lignes,
• Taper un point-virgule (;) pour passer dans l'argument du nombre de colonnes,
• Inscrire de nouveau le chiffre 5 pour compléter la suite sur cinq colonnes,
• Taper un point-virgule (;) pour passer dans l'argument du point de départ,
• Comme précédemment, taper le nombre 50 pour la faire débuter à cet indice,
• Taper un point-virgule (;) pour passer dans l'argument du pas de l'incrémentation,
• Taper le nombre 10 pour faire progresser cette suite de 10 unités en 10 unités,
• Fermer la parenthèse de la fonction Sequence et valider la formule par la touche Entrée,

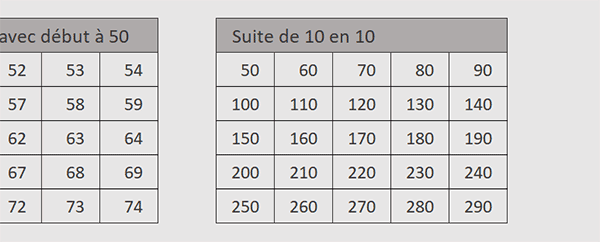
Nous obtenons bien une suite de 25 nombres, répartis sur 5 colonnes et 5 lignes, tous espacés les uns des autres par un différentiel de 10 unités, comme demandé dans le quatrième paramètre de la fonction Sequence.