Synthèse sur l'absentéisme et l'assiduité des salariés

Pour partager cette vidéo sur les réseaux sociaux ou sur un site, voici son url :


Sujets que vous pourriez aussi aimer :


Synthèse d'assiduité

Dans cette formation, nous apportons la solution pour repérer les salariés les plus souvent absents ainsi que les salariés les plus assidus. Ces données statistiques sont toujours intéressantes à interpréter avec du recul. Elles dévoilent rapidement quels sont les éléments, bons ou moins bons, qui se détachent des autres.



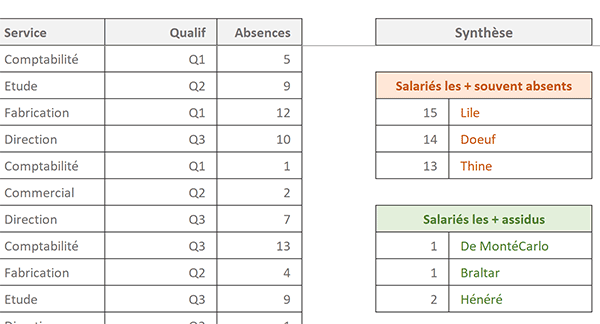
Dans l'exemple finalisé, illustré par la capture ci-dessus, une base de données Excel recense les salariés de l'entreprise. Pour chacun d'entre eux, le nombre d'absences est consolidé dans la dernière colonne du tableau. Sur la droite de ce dernier, une synthèse dynamique précieuse est livrée. Elle extrait dans l'ordre les jours d'absences les plus nombreux, ainsi que les moins nombreux dans un deuxième temps. A chacun d'entre eux, sont associés les employés concernés. Il en résulte une synthèse riche d'enseignements pour le responsable.

Source et principe
Pour apporter cette solution par les calculs, nous devons commencer par récupérer cette base de données.

• Télécharger le classeur premieres-valeurs-remarquables.xlsx en cliquant sur ce lien,
• Double cliquer sur le fichier téléchargé pour l'ouvrir dans Excel,
• Puis, cliquer sur le bouton Activer la modification du bandeau de sécurité,

C'est sur la droite du tableau que nos travaux doivent se concentrer, plus précisément entre les colonnes H et I.

Entre les lignes 6 et 8, nous devons extraire dynamiquement et dans l'ordre, les nombres d'absences les plus importants puis leur associer les salariés impliqués dans la colonne voisine.

A l'inverse, entre les lignes 11 et 13, nous devons extraire dynamiquement et dans l'ordre, les nombres d'absences les moins importants puis leur associer les employés concernés.

Nous allons essayer d'appliquer les techniques matricielles.

Premières valeurs seuilles
Avant de commencer, vous constaterez que chaque colonne du tableau est nommée en fonction de son titre de champ. Vous pouvez le remarquer en déployant la liste déroulante de la zone Nom.

Excel offre deux fonctions permettant de connaître les valeurs remarquables au milieu d'autres données. Outre les fonctions Max et Min qui sont binaires, il existe les fonctions Petite.Valeur et Grande.Valeur :

=PETITE.VALEUR(Plage_de_cellules; Rang)
=GRANDE.VALEUR(Plage_de_cellules; Rang)

Sur une plage de cellules passée en premier paramètre, elles permettent respectivement d'extraire l'une des plus petites ou l'une des plus grandes valeurs, selon un rang passé en second paramètre. Il peut ainsi s'agir de la deuxième plus petite ou plus grande donnée. Elles représentent donc des déclinaisons intéressantes des fonctions Min et Max qui extraient uniquement la plus petite ou la plus grande valeur.

Mais la synthèse demandée pose une problématique. Il est question d'extraire les 3 premières valeurs seuilles, qu'il s'agisse des plus grandes ou des plus petites.

Certes, nous pourrions très bien inscrire la formule suivante en H6 : =GRANDE.VALEUR(Absences;1). Pour les deux lignes suivantes, il suffirait de modifier le chiffre 1 par le 2 puis par le 3. Et nous pourrions rééditer ce principe à partir de la cellule H11 avec la fonction PETITE.VALEUR. Mais ce calcul n'a rien de dynamique puisqu'il ne peut être répliqué sans intervention.

Nous proposons donc de raisonner sur des matrices avec une technique très particulière mais qui mérite d'être connue. Sur l'ensemble de la colonne des absences, nous allons scruter la présence des trois plus petites valeurs pour commencer. Et lorsqu'elles seront décelées, nous devrons les extraire. Pour cela, nous avons besoin des fonctions Index et Equiv :

=Equiv(Valeur_cherchée; Colonne_de_recherche; Mode_de_recherche)
=Index(Base_de_données; ligne; colonne)

C'est la fonction Index qui permet d'extraire les informations situées aux croisements de lignes et de colonnes. Tandis que la colonne est connue, la ligne dépend de la position de ces valeurs seuilles à repérer. C'est pourquoi, nous devons exploiter la fonction Equiv pour retourner cette information variable.

• Sélectionner les plus grandes absences à extraire, soit la plage de cellules H6:H8,

Malgré cette sélection de cellules, nous allons poser le calcul comme si seule la première d'entre elles était sélectionnée.

• Taper le symbole égal (=) pour initier le calcul,
• Saisir la fonction d'extraction suivie d'une parenthèse, soit : Index(,
• Désigner la colonne des absences par son nom, soit : Absences,
• Taper un point-virgule (;) pour passer dans l'argument de la ligne,
• Saisir la fonction cherchant cette information, suivie d'une parenthèse, soit : Equiv(,
• Saisir ensuite la fonction statistique suivie d'une parenthèse, soit : Grande.Valeur(,
• Désigner la plage de recherche par son nom, soit : Absences,
• Taper un point-virgule (;) pour passer dans l'argument du rang,
• Puis, saisir la syntaxe suivante :{1;2;3},

C'est elle l'astuce très particulière qui va permettre de raisonner sur des matrices. L'énumération des trois premiers rangs est fournie entre accolades. Explicitement, nous indiquons que nous souhaitons extraire dans l'ordre, la première valeur la plus grande, puis la deuxième et enfin la troisième.

• Fermer la parenthèse de la fonction Grande.Valeur,
• Taper un point-virgule (;) pour passer dans l'argument de la colonne de recherche,
• Désigner de nouveau la plage des absences par son nom, soit : Absences,
• Taper un point-virgule suivi du chiffre zéro, soit : ;0, pour un mode de recherche exact,
• Fermer la parenthèse de la fonction Equiv,
• Taper un point-virgule (;) pour passer dans l'argument de la colonne pour la fonction Index,
• Saisir le chiffre 1 puisque seule une colonne est désignée pour l'extraction (absences),
• Fermer la parenthèse de la fonction Index,
• Puis, valider nécessairement la formule par le raccourci clavier CTRL + MAJ + Entrée,

C'est lui qui rend la formule matricielle. Vous notez d'ailleurs la présence des accolades encadrant la syntaxe dans la barre de formule des cellules des résultats.

{=INDEX(Absences; EQUIV(GRANDE.VALEUR(Absences; {1;2;3}); Absences; 0); 1)}

Remarque : La touche Maj est aussi connue sous sa désignation anglaise Shift.

Quoiqu'il en soit, avec une seule formule, les résultats tombent. Nous obtenons bien les trois plus grands nombres d'absences, qui plus est classés dans l'ordre décroissant.

De fait, il suffit de répliquer la même syntaxe sur la plage de cellules H11:H13, sans oublier de remplacer la fonction Grande.Valeur par la fonction Petite.Valeur :

{=INDEX(Absences; EQUIV(PETITE.VALEUR(Absences; {1;2;3}); Absences; 0); 1)}

Nous obtenons bien les trois plus petits nombres d'absences classés dans l'ordre croissant.



Nous aurions aussi pu aboutir la solution avec des techniques usuelles de calcul :

=INDEX(Absences; EQUIV(GRANDE.VALEUR(Absences; LIGNE(A1)); Absences; 0); 1)
=INDEX(Absences; EQUIV(PETITE.VALEUR(Absences; LIGNE(A1)); Absences; 0); 1)

L'astuce réside dans l'utilisation de la fonction Ligne dans le paramètre du rang des fonctions statistiques. Pour le premier calcul, nous lui passons la cellule A1. La fonction Index demande donc d'extraire la plus grande ou la plus petite valeur. En répliquant la formule sur les lignes du dessous, A1 se transforme en A2 puis A3. Nous demandons ainsi d'extraire les valeurs seuilles suivantes.

Mais, nous le savons, les calculs matriciels permettent d'aller au-delà des limites rencontrées par les calculs classiques. C'est pourquoi il est important de continuer l'entraînement.

Absences les plus fréquentes et assiduités
Finalement, nous pourrions penser que le plus dur est fait. Nous sommes tentés d'ajuster la colonne de recherche pour produire l'extraction des salariés, selon le même mode opératoire.

• Sélectionner la cellule H6,
• Dans sa barre de formule, sélectionner l'intégralité de la syntaxe,
• La copier par le raccourci clavier CTRL + C,
• Puis, sortir de la barre de formule nécessairement par le raccourci CTRL + MAJ + Entrée,
• Sélectionner alors la plage de cellules I6:I8,
• Dans la barre de formule, coller (CTRL + V) la syntaxe copiée,
• Remplacer la première plage Absences par Nom,
• Puis, valider nécessairement la formule par le raccourci clavier CTRL + MAJ + Entrée,

{ =INDEX(Nom; EQUIV(GRANDE.VALEUR(Absences; {1;2;3}); Absences; 0);1)}

Nous obtenons bien l'extraction des salariés les plus souvent absents, dans l'ordre imposé par le premier calcul.

Dans la foulée donc, et selon la même technique, il apparaît opportun de construire la formule d'extraction suivante, sur la plage de cellules I11:I13 :

{ =INDEX(Nom; EQUIV(PETITE.VALEUR(Absences; {1;2;3}); Absences; 0);1)}



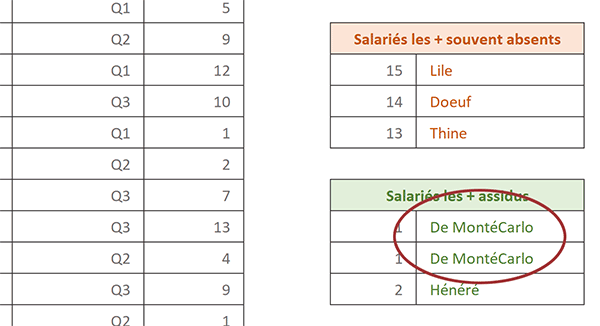
Mais à validation, un problème surgit. En effet, deux employés possèdent le même nombre d'absences. Les fonctions d'extraction s'arrêtent sur la première valeur trouvée et extraient seulement le premier d'entre eux.

Nous allons donc devoir contourner le problème.

Différencier les répétitions
A défaut de solution matricielle, nous allons exécuter des calculs intermédiaires de repérage. Dans l'extraction des valeurs seuilles, nous devons identifier les répétitions. Pour cela, nous proposons de concaténer les nombres d'absences extraits par leurs nombres de répétions. Un autre calcul intermédiaire doit faire de même en regard de la base de données afin de concaténer les nombres équivalents avec leurs répétitions. L'extraction pourra alors naturellement se faire sur ces correspondances.

• Sélectionner la cellule G6 et construire le calcul suivant:

=SI(ET(H6=H4; H6=H5); H6&3; SI(H6=H5; H6&2; H6&1))

• Après validation, tirer la poignée du résultat sur les deux lignes du dessous (G7 et G8),

Nous comparons le nombre de la cellule voisine avec les valeurs inscrites dans les deux cellules du dessus. Si une double répétition est constatée, nous le concaténons avec le chiffre 3 pour en informer les calculs à suivre. Sinon, si seule une répétition est observée, nous le concaténons avec le chiffre 2. Dans le cas restant, nous le concaténons avec le chiffre 1 pour indiquer qu'il s'agit bien du premier et de l'original. C'est cette différenciation, qui va nous permettre d'extraire les salariés précisément associés en cas de redondances.

Remarque : Concernant la cellule H5, en raison de la fusion, il est préférable de saisir ses coordonnées plutôt que de la cliquer dans la construction de la syntaxe.

La logique du calcul doit être répliquée, par copier-coller, sur le petit tableau du dessous pour les salariés les plus assidus. La formule doit être établie en cellule G11 puis répliquée sur les deux lignes du dessous :

=SI(ET(H11=H9; H11=H10); H11&3; SI(H11=H10; H11&2; H11&1))



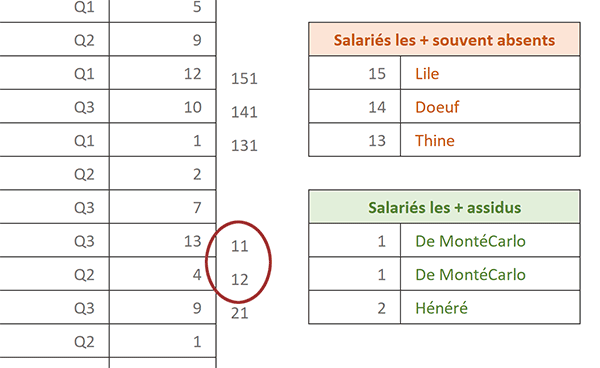
Grâce à cette astuce conditionnelle de repérage, vous constatez que les deux salariés les plus assidus sont cette fois clairement différenciés.

Nous devons appliquer sensiblement la même logique sur la base de données afin de différencier les salariés pour lesquels les nombres d'absences sont équivalents. L'astuce consiste à dénombrer ces valeurs sur une plage de cellules qui progresse en même temps que le calcul. Ainsi, la concaténation avec la répétition peut s'opérer.

• Sélectionner la première cellule en regard de la base de données, soit A4,
• Construire la formule suivante :

=SI(NB.SI($F$4:F4; F4)>0; F4&NB.SI($F$4:F4; F4);'')

• Après validation, double cliquer sur la poignée du résultat pour répliquer la logique,

Dans le critère de la fonction conditionnelle, nous exploitons la fonction de dénombrement Nb.Si. Nous cherchons à comptabiliser les répétitions du nombre d'absence (F4) pour l'enregistrement concerné. Pour le premier calcul, ce dénombrement s'effectue sur la plage F:4:F4, soit uniquement la première cellule des absences. Mais, sa borne supérieure est figée ($F$4) tandis que sa borne inférieure est libre de se déplacer (F4). De fait, avec la réplication de la formule sur les lignes du dessous, cette plage grandit au fur et à mesure : $F$4:F5 puis $F$4:F6 etc... C'est ainsi que les répétitions sont différenciées des originaux. Lorsque la redondance est avérée, nous concaténons le nombre d'absences avec son nombre de répétitions : F4&NB.SI($F$4:F4; F4). Le cas échéant, nous n'inscrivons rien. Ce cas ne peut se produire. Etant donnée la plage analysée, la valeur est comptée au moins une fois.

Extraire les noms des salariés
Grâce à cette identification, nous allons désormais pouvoir faire la correspondance entre les numéros des tableaux des absences et ceux de la base de données. C'est la fonction Excel Index qui permet d'isoler une information située au croisement d'une ligne et d'une colonne.

=Index(Base_de_recherche; Ligne; Colonne)

La colonne est connue. Elle est donc fixe. Il s'agit de la colonne B, soit de la première dans la base de données. En revanche, la ligne est variable. Elle dépend de la position trouvée pour le numéro correspondant. Pour isoler cette position, nous allons exploiter la fonction Equiv.

=Equiv(Valeur_cherchée, Colonne_de_recherche; Mode_de_correspondance)

• Sélectionner la plage de cellules I6:I8,
• Enfoncer la touche Suppr pour effacer le précédent calcul matriciel,
• Faire de même sur la plage de cellules I11:I13,
• Sélectionner la cellule I6 du premier salarié à trouver,
• Taper le symbole égal (=) pour initier le nouveau calcul,
• Saisir la fonction d'extraction suivie d'une parenthèse, soit : Index(,
• Désigner l'intégralité de la colonne des noms par son étiquette, soit : B:B,
• Taper un point-virgule (;) pour passer dans l'argument de la ligne à trouver,
• Saisir la fonction cherchant cette position, suivie d'une parenthèse, soit : Equiv(,
• Cliquer sur le premier numéro concaténé à trouver, soit la cellule G6,
• Taper un point-virgule (;) pour passer dans l'argument de la colonne de recherche,
• Désigner l'intégralité de la colonne du calcul intermédiaire par sont étiquette, soit : A:A,
• Taper un point-virgule suivi du chiffre zéro, soit : ;0, pour réaliser une recherche exacte,
• Fermer la parenthèse de la fonction Equiv,
• Taper un point-virgule (;) pour passer dans l'argument de la colonne pour la fonction Index,
• Saisir le chiffre 1 pour désigner l'unique rangée spécifiée,
• Fermer la parenthèse de la fonction Index,
• Valider le calcul par le raccourci clavier CTRL + Entrée,
• Puis, répliquer la logique du calcul sur les cellules I7 et I8 avec la poignée du résultat,

Nous obtenons sans surprise strictement la même extraction des salariés que celle établie par les calculs matriciels. Pour les employés les plus souvent absents, il n'existe en effet aucune répétition sur le nombre des absences.

• Ce calcul doit être adapté en cellule I11 : =INDEX(B:B; EQUIV(G11; A:A; 0); 1),
• Puis, il doit être répliqué avec la poignée sur les deux cellules du dessous I12 et I13,

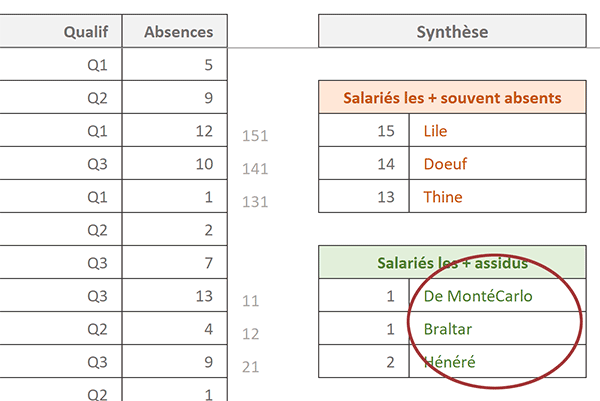
Cette fois, une différence notable est à observer. Nous avons réussi à différencier les salariés associés au même nombre d'absences. De fait, nous avons produit l'extraction chirurgicale souhaitée, grâce à ces calculs intermédiaires de repérage.

Nous avons donc réussi à construire une solution fort intéressante pour évaluer l'absentéisme au sein de l'entreprise.