Somme Excel sur une colonne ou une ligne sur deux

Pour partager cette vidéo sur les réseaux sociaux ou sur un site, voici son url :


Sujets que vous pourriez aussi aimer :


Opérations sur des colonnes alternées

Certains tableaux de synthèse présentent des structures denses et parfois complexes. Les informations ne sont pas forcément ordonnées dans un ordre logique pour les calculs.



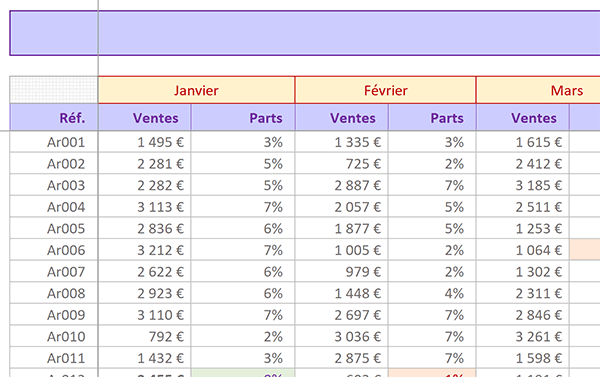
C'est le cas du tableau dont un extrait est proposé par la capture ci-dessus. Les ventes réalisées par articles sont énumérées par mois, une colonne sur deux. En bout de chaque ligne, la synthèse par article est attendue. Cette formation met la lumière sur une technique de calcul capable de s'adapter à ces configurations. L'objectif est de contourner les multi-sélections fastidieuses et parfois précaires, lorsqu'elles sont nombreuses.

Source et présentation de l'objectif
Pour réaliser ces démonstrations, nous proposons tout d'abord de réceptionner les données utiles.

• Télécharger le classeur bilan-calculs-lignes.xlsx en cliquant sur son lien,
• Double cliquer sur le fichier récupéré pour l'ouvrir dans Excel,
• Puis, cliquer sur le bouton Activer la modification du bandeau de sécurité,

Nous réceptionnons donc un tableau annuel de suivi des ventes. Les produits sont listés en colonne B. Pour chaque mois de l'année et à raison d'une colonne sur deux, sont livrées les ventes réalisées pour chacun. En effet, pour chaque mois, une autre colonne est destinée à rendre compte de la part que représente chaque article par rapport à l'ensemble des produits.



De fait, il faut atteindre la colonne AA pour trouver la rangée du calcul de synthèse attendu. Il s'agit de consolider les ventes réalisées par articles au cours de l'année. En d'autres termes, nous devons réaliser la somme des ventes sur chaque ligne, mais une colonne sur deux.

Bien sûr, nous pourrions engager la fonction Somme et sélectionner tour à tour les cellules impliquées. Mais cette méthode présente deux inconvénients. Sur la base de colonnes désignées statiquement, le résultat obtenu ne pourrait évoluer dynamiquement. Nous pouvons très bien imaginer que de nouvelles rangées sont ajoutées régulièrement. De plus, cette technique est à la fois fastidieuse et périlleuse. Le tableau est large. Il convient d'être extrêmement minutieux. Mais le risque d'omettre une rangée est grand.

Calcul matriciel
La technique est particulière. Elle consiste à exploiter la fonction Excel SommeProd, mais de façon inhabituelle. La fonction SommeProd agit sur des matrices. Pour chaque ligne respective, elle multiplie les valeurs puis somme le tout.

=SommeProd(Matrice1; Matrice2 ; ... ; MatriceN)

On l'utilise couramment pour calculer la moyenne générale d'un étudiant, en tenant compte des coefficients attachés à chaque matière. Chaque note est multipliée par son coefficient et additionnée aux autres, calculées de la même façon. Le tout est alors divisé par la somme des coefficients, conduisant à la moyenne générale.

Mais ici, l'objectif est de repérer chaque colonne concernée par le chiffre 1. Il doit faire office de valeur dans la première matrice désignée en argument de la fonction SommeProd. La deuxième matrice doit conserver ses valeurs d'origine. Ainsi, la fonction SommeProd réalisera la multiplication de chaque vente, avec le chiffre 1 de chaque colonne identifiée. Il en résultera la somme des ventes pour chaque article.

En premier argument, nous devons donc spécifier une matrice retravaillée. Et ce sont les fonctions Excel MOD et COLONNE qui vont nous y aider. La première retourne une valeur booléenne indiquant s'il existe un reste à la division. La seconde renvoie l'indice de colonne d'une cellule ou d'une plage de cellules. Nous lui spécifierons la largeur du tableau sur laquelle travailler, soit la plage C7:Z7. Pour chaque rangée, si le reste de la division par le chiffre 2 est nul, nous saurons qu'il s'agit d'une colonne paire. Dans le cas contraire, nous saurons qu'il s'agit d'une colonne impaire. Et ce sont précisément ces dernières qui nous intéressent. La première vente débute en effet en colonne C, soit à l'indice impair 3.

• Sélectionner la première somme à trouver, soit la cellule AA7,
• Taper le symbole égal (=) pour initier la formule,
• Saisir la fonction matricielle suivie d'une parenthèse, soit : SommeProd(,
• Puis, à gauche de la barre de formule, cliquer sur l'icône Insérer une fonction,

Cette action a pour effet de déclencher l'assistant fonction. Il va nous aider à mieux appréhender le raisonnement du calcul alambiqué que nous sommes en train d'entreprendre.

• Dans la zone de saisie Matrice1, ouvrir la parenthèse,
• Saisir la fonction du reste de la division, suivie d'une parenthèse, soit : Mod(,
• Taper la fonction pour l'indice de colonne, suivie d'une parenthèse, soit : Colonne(,
• Désigner ou saisir la première ligne complète, soit la plage de cellules C7:Z7,
• Fermer la parenthèse de la fonction Colonne,
• Taper un point-virgule (;) pour passer dans le deuxième argument de la fonction Mod,
• Saisir le chiffre 2, pour calculer le reste de la division par 2,
• Fermer la parenthèse de la fonction Mod,
• Taper le symbole égal suivi du chiffre 1, soit : =1,

Par cette égalité, nous désignons la plage de cellules à précisément repérer. Sur cette largeur, à chaque fois que la fonction Mod indique qu'un reste à la division persiste, cela signifie qu'il s'agit d'une colonne impaire.

• Fermer la parenthèse de la factorisation,

L'assistant fournit aussitôt des indications fort précieuses. Il interprète ce premier calcul, fruit d'un raisonnement matriciel.



Et en effet, les résultats sont livrés sous forme de tableau, sur la droite de la zone Matrice1. En commençant par la première colonne (C), le repère booléen intervient une fois sur deux. Grâce à l'égalité de ce calcul, il identifie donc toutes les colonnes impaires, en partant de la colonne C.

La valeur booléenne Vrai équivaut à 1. La valeur booléenne Faux équivaut à 0. Mais, pour qu'Excel interprète réellement ces données comme des chiffres, nous avons besoin de forcer le calcul.

• A la suite de la syntaxe, taper le symbole de l'étoile suivi du chiffre 1, soit : *1,

Instantanément, les valeurs numériques associées remplacent les valeurs booléennes dans les résultats de l'interprétation fournis par l'assistant.

Désormais donc, en renseignant la deuxième matrice en second argument, chaque valeur de cette dernière sera un coup sur deux multipliée par un, pour les colonnes impaires, et un coup sur deux multipliée par 0, pour les colonnes paires. De fait, les parts ne seront pas considérées dans l'addition finale. Et cette seconde matrice est identique à la première.

• Cliquer dans la zone Matrice2 pour l'activer,
• Sélectionner ou saisir les références de la ligne complète, soit la plage de cellules C7:Z7,

Instantanément, les indications de l'assistant s'actualisent. Le tableau des valeurs est représenté en regard de la zone Matrice2. Les pourcentages y sont affichés dans leur version numérique brute. Et selon le mécanisme de la fonction SommeProd, chacun d'entre eux sera multiplié par la ligne correspondante de la première matrice, soit zéro. A ce titre, vous constatez le résultat de synthèse fournit en avant-première, en bas de la boîte de dialogue. Il s'agit de la somme alternée, soit de l'addition réalisée une colonne sur deux, en débutant depuis une rangée impaire.

• Cliquer sur le bouton Ok de l'assistant pour valider la formule,

Effectivement, le résultat attendu s'inscrit dans la cellule du calcul. La formule est terriblement efficace mais fort inhabituelle. A titre de vérification, si vous englobez toutes les cellules des colonnes impaires de la ligne 7 dans une même sélection, grâce à la touche CTRL, vous remarquez que l'information de synthèse fournie par Excel dans sa barre d'état, recoupe celle du résultat dynamique.

• Double cliquer sur la poignée du résultat pour répliquer la logique sur tout le tableau,

Nous avons donc apporté la solution de la somme dynamique alternée. Et à ce titre, le mécanisme est tout à fait identique pour produire l'addition une ligne sur deux. Même si le contexte de ce tableau ne s'y prête pas, nous proposons de faire la somme des ventes, en colonne C pour les lignes paires.

• Sélectionner par exemple la cellule C29,
• Taper le symbole égal (=) pour débuter le calcul,
• Saisir la fonction matricielle suivie d'une parenthèse, soit : SommeProd(,
• Cliquer alors sur le bouton Insérer une fonction pour déclencher l'assistant,
• Dans la zone Matrice1, ouvrir la parenthèse de la factorisation,
• Saisir la fonction pour le reste de la division, suivie d'une parenthèse, soit : Mod(,
• Saisir la fonction de l'indice de ligne suivie d'une parenthèse, soit : Ligne(,
• Sélectionner la rangée des ventes, soit la plage de cellules C7:C26,
• Fermer la parenthèse de la fonction Ligne,
• Taper un point-virgule (;) suivi du chiffre 2 pour la division, soit : ;2,
• Fermer la parenthèse de la fonction Mod,
• Taper le symbole égal (=) suivi du chiffre zéro, soit : =0,

En effet, cette fois nous souhaitons identifier les lignes paires et non plus les lignes impaires. Le reste de la division par 2 doit donc être nul.

• Fermer la parenthèse de la factorisation,
• Taper le symbole de l'étoile suivi du chiffre 1, soit : *1,

C'est ainsi que nous convertissons les valeurs booléennes de repérage par leurs équivalents numériques.

• Cliquer dans la zone Matrice2 pour l'activer,
• Sélectionner de nouveau les ventes, soit la plage de cellules C7:C26,

Là encore, l'assistant fournit ses interprétations en amont. En regard de la zone Matrice1, le tableau résultant prouve que seules les lignes paires seront engagées dans l'addition.

• Cliquer sur le bouton Ok de la boîte de dialogue pour valider le calcul,

Le résultat est fort logiquement inférieur à l'addition fournie deux lignes plus haut par somme officielle. Une fois encore, si vous réunissez les cellules des lignes paires dans une même sélection, vous constatez que le résultat de synthèse dans la barre d'état est identique à la formule de la somme alternée.