Comprendre les calculs matriciels avec Excel

Pour partager cette vidéo sur les réseaux sociaux ou sur un site, voici son url :


Sujets que vous pourriez aussi aimer :


Comprendre les calculs matriciels

Les calculs matriciels sont d'une redoutable efficacité. Ils offrent une grande puissance et livrent souvent des solutions directes, plus difficilement accessibles par les formules classiques. Mais leur construction peut sembler complexe à appréhender.



Dans ce premier volet, nous proposons de décortiquer leur logique afin de les démystifier.

Source et présentation du principe
Pour la découverte des formules matricielles, nous proposons d'appuyer nos travaux sur des données existantes.

• Télécharger le classeur decouvrir-calculs-matriciels.xlsx en cliquant sur ce lien,
• Double cliquer sur le fichier téléchargé pour l'ouvrir dans Excel,
• Puis, cliquer sur le bouton Activer la modification du bandeau de sécurité,

Nous réceptionnons un classeur muni de deux feuilles nommées respectivement Moyenne et Remises. Grâce aux tableaux qu'elles proposent, nous allons pouvoir nous exercer sur la construction et la compréhension des calculs matriciels.



Le tableau de la feuille Moyenne propose de réaliser le calcul de la moyenne générale, selon les notes obtenues par l'étudiant. Mais chaque matière est associée à un coefficient. Elles ne pèsent donc pas toutes le même poids. Et pour considérer ces coefficients, c'est une moyenne pondérée qui doit être calculée.

Le tableau de la feuille Remises énumère des prix de vente d'articles. Des réductions accordées en pourcentages doivent leur être appliquées. Elles diffèrent selon le client concerné. La solution doit être livrée par une unique formule à répliquer sur l'ensemble du tableau.

Calcul d'une moyenne pondérée
La moyenne pondérée consiste dans un premier temps à multiplier chaque note par son coefficient. Les résultats obtenus doivent alors être additionnés. Cette somme doit enfin être divisée par l'addition des coefficients. Il en résulte la moyenne générale. Pour bien comprendre l'intérêt et la puissance des calculs matriciels, il est important de réaliser premièrement l'opération grâce à des formules classiques décomposées.

• En bas de la fenêtre Excel, cliquer sur l'onglet Moyenne pour revenir sur sa feuille,

Le procédé est le suivant :

• En cellule D5, la notre doit être multipliée par son coefficient : =B5*C5,
• Le calcul validé doit être répliqué en hauteur jusqu'en cellule D9,

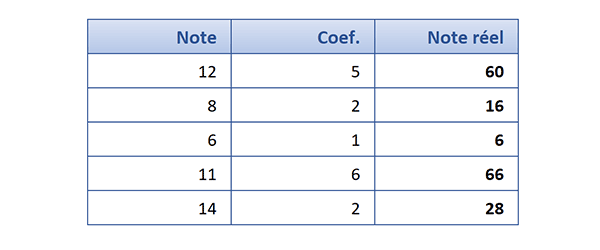
Il en résulte les véritables moyennes ramenées sur une échelle ou les valeurs peuvent être évaluées.

• La somme de ces notes doit ensuite être produite en D11 selon la formule suivante :

=SOMME(D5:D9)

• La moyenne pondérée peut alors être livrée en D12 en divisant ce résultat par la somme des coefficients :

=D11/SOMME(C5:C9)

Pour obtenir cette moyenne pondérée par les formules classiques, nous avons dû décomposer le calcul en trois étapes.

Ces étapes peuvent être court-circuitées grâce aux calculs matriciels.

Calculer la somme des multiplications
Pour entrer de plein pied dans la philosophie des calculs matriciels, nous proposons de réaliser directement le calcul de la somme en cellule D11. Cela signifie que nous devons ignorer l'étape intermédiaire du calcul produit sur la plage de cellules D5:D9.

Un calcul matriciel simple comme ici consiste à raisonner sur deux rangées dont il s'agit de multiplier entre elles les valeurs respectives, soit ligne à ligne. Ces deux rangées ou matrices ne sont autres que les plages de cellules B5:B9 et C5:C9. Comme la somme de ces résultats doit être produite dans le même temps, la multiplication des matrices doit être imbriquée dans la fonction Somme.

• Supprimer le résultat de la somme en cellule D11,
• Taper le symbole égal (=) pour initier la syntaxe du calcul matriciel,
• Saisir la fonction d'addition suivie d'une parenthèse, soit : Somme(,
• Ouvrir une nouvelle parenthèse pour la première matrice à désigner,
• Sélectionner toutes les notes, soit la plage de cellules B5:B9,
• Fermer alors la parenthèse de cette matrice,
• Taper le symbole de l'étoile (*) pour enclencher la multiplication,
• Ouvrir une autre parenthèse pour accueillir la seconde matrice,
• Sélectionner tous les coefficients, soit la plage de cellules C5:C9,
• Fermer la parenthèse de cette seconde matrice,
• Puis, fermer la parenthèse de la fonction Somme,

L'instant crucial d'un calcul matriciel se joue au moment de sa validation. Il ne peut être validé comme un calcul classique. C'est un raccourci clavier particulier qui indique à Excel de réaliser les opérations entre les deux matrices, ligne à ligne.

• Valider la formule matricielle par le raccourci clavier CTRL + MAJ + Entrée,

La touche Maj est aussi connue sous la désignation anglaise : Shift. Sans cette combinaison de touches et dans ce contexte, la formule aurait généré une erreur.



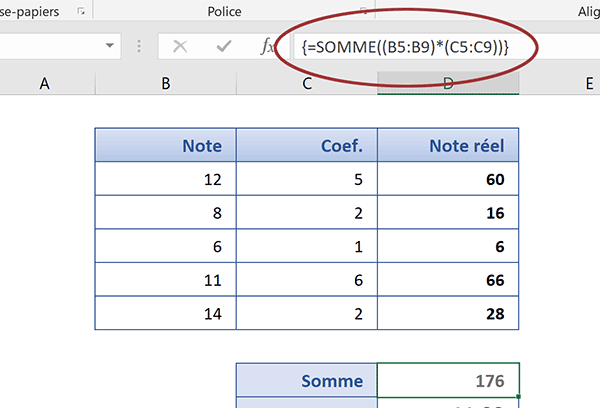
Mais grâce à elle et à la syntaxe, le calcul matriciel est généré. Et comme vous pouvez le voir, sans étape intermédiaire, il conduit exactement au même résultat que le précédent calcul.

Si vous consultez la barre de formule de la cellule du calcul, vous remarquez la présence d'accolades :

{=SOMME((B5:B9)*(C5:C9))}

Ce sont elles qui indiquent et obligent les opérations à raisonner sur des matrices, telles que nous les avons désignées entre parenthèses. La moyenne pondérée se déduit naturellement dans la cellule du dessous. Nous aurions d'ailleurs pu intégrer cette division directement dans la formule matricielle.

Faire la somme des produits
Nous venons de réaliser un calcul matriciel manuel. Et vous en conviendrez, sa méthode de validation est tout à fait particulière. Excel offre aussi une fonction raisonnant naturellement sur des matrices. Il s'agit de la fonction SommeProd : =SommeProd(Matrice1; Matrice2; ...; MatriceN). Elle porte bien son nom puisqu'elle réalise la somme des produits. Il suffit simplement d'énumérer les matrices concernées par le calcul, en paramètres de la fonction. En outre, elle offre l'avantage de valider la formule classiquement.

• Supprimer le précédent résultat en cellule D11,
• Taper le symbole égal (=) pour débuter la nouvelle formule matricielle,
• Taper le nom de la fonction suivi d'une parenthèse, soit : SommeProd(,
• Désigner la première matrice, soit la plage de cellules B5:B9,
• Taper un point-virgule (;) pour poursuivre l'énumération,
• Désigner alors la seconde matrice, soit la plage de cellules C5:C9,
• Fermer la parenthèse de la fonction SommeProd,
• Puis, valider naturellement le calcul par la touche Entrée du clavier,

Nous obtenons une troisième fois le même résultat. La fonction SommeProd a permis d'engager le calcul matriciel de la multiplication ligne à ligne. A l'issue, l'addition des résultats est livrée. Et cette fois, il n'est nul nécessaire de valider la formule avec une combinaison de touches particulière.

Calcul matriciel des remises
Dans ce volet de découverte, il nous reste à réaliser une mise en pratique spécifique.

• En bas de la fenêtre Excel, cliquer sur l'onglet Remises pour activer sa feuille,

Des prix de vente sont énumérés en colonne B du tableau proposé. Des taux de remises différents sont listés en ligne 4. Il s'agit de concessions accordées aux clients selon leur importance. Bien sûr, l'idée est de produire le calcul de toutes les remises avec une seule formule. Et pour bien comprendre une fois de plus la puissance des formules matricielles, nous proposons de débuter par la méthode classique de calcul.

La procédure est celle-ci :

• La formule suivante doit être bâtie en cellule C5 : =$B5*C$4,

Il s'agit d'une multiplication entre le premier prix de vente et le premier taux. Et comme vous pouvez le voir, nous exploitons les références mixtes. Les prix de vente sont énumérés dans une seule et même colonne. Nous figeons donc la colonne de sa cellule ($B5). Les taux de remise sont listés dans une seule et même ligne. Nous figeons donc la ligne de sa cellule (C$4).

Ensuite, il convient de répliquer la formule sur l'intégralité du tableau.

• Pour cela, il faut tirer la poignée du résultat à l'horizontale jusqu'en cellule F5,
• Puis, il s'agit de tirer la poignée de la sélection active à la verticale, jusqu'en cellule F8,

Nous aurions aussi pu présélectionner l'ensemble des cellules vides, bâtir le calcul à l'identique et le valider par le raccourci clavier CTRL + Entrée. Ainsi, nous l'aurions répliqué dans le même temps. Ces techniques précieuses sont notamment enseignées dans le petit livre gratuit pour maîtriser les calculs avancés avec Excel.



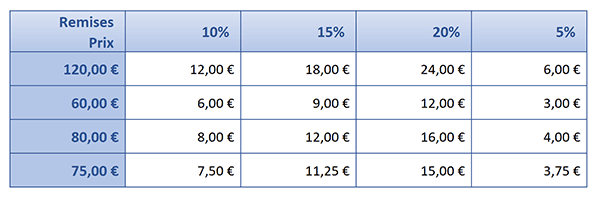
Bref et comme vous le constatez, nous obtenons bien tous les calculs des remises accordées. Et ces résultats sont parfaitement cohérents.

Maintenant il est temps d'aborder la solution matricielle pour comparer l'efficacité. Il s'agit d'engager la multiplication des valeurs respectives entre chaque matrice. Mais l'une d'entre elles est transposée. Nous allons le voir, dans le raisonnement matriciel, cette configuration n'est absolument pas conflictuelle. Les éléments vont être passés en revue les uns après les autres et considérés entre eux.

• Sélectionner la plage de cellule C5:F8,
• Enfoncer la touche Suppr du clavier pour éliminer les précédents résultats,

Nous allons conserver l'intégralité de la plage sélectionnée pour bâtir cette formule. Et à ce titre, vous remarquez que la première d'entre elles, la cellule C5, n'apparaît par surlignée. Excel indique qu'il s'agit de la case considérée par défaut.

• Taper le symbole égal (=) pour initier le calcul matriciel,
• Ouvrir une parenthèse pour accueillir la première matrice,
• Sélectionner tous les prix de vente, soit la plage de cellules B5:B8,
• Fermer la parenthèse de cette première matrice,
• Taper le symbole de l'étoile (*) pour enclencher la multiplication,
• Ouvrir une nouvelle parenthèse pour accueillir la seconde matrice,
• Sélectionner tous les taux de remise, soit la plage de cellules C4:F4,
• Fermer la parenthèse de cette seconde matrice,
• Puis, valider la formule matricielle par le raccourci clavier CTRL + MAJ + Entrée,

Nous obtenons exactement les mêmes résultats, automatiquement répliqués sur tout le tableau. De plus, la formule est encore plus simple de mise en oeuvre.

Une fois validée, sa syntaxe matricielle est la suivante : {=(B5:B8)*(C4:F4)}.

Dans les prochains volets, nous veillerons à mettre en pratique ces acquis. Et nous constaterons très vite les intérêts que procurent ces formules matricielles dans des mises en situation professionnelles.