Calculs sur des plages alternées de longueur dynamique

Pour partager cette vidéo sur les réseaux sociaux ou sur un site, voici son url :


Sujets que vous pourriez aussi aimer :


Calculs toutes les N valeurs

Pour effectuer des opérations toutes les N valeurs, il faut être en mesure de réaliser un décalage cyclique sur les données impliquées dans la formule. Ces opérations alternées concernent tout type de calcul.



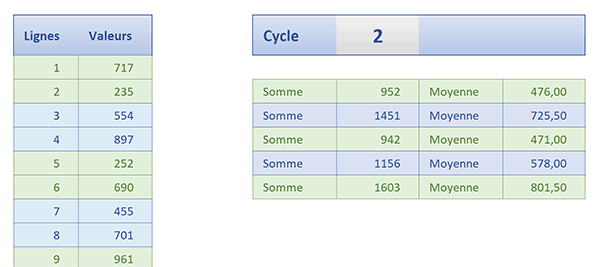
Sur l'exemple illustré par la capture, en fonction d'un intervalle numérique inscrit par l'utilisateur, nous calculons les sommes et moyennes cycliques, respectant ce palier. Et bien entendu, si nous modifions cette valeur, les résultats s'adaptent automatiquement en ajustant la hauteur des plages alternées.

Source et présentation
Pour réaliser ces travaux, nous proposons de récupérer une source offrant des valeurs numériques à manipuler.

• Télécharger le classeur calculs-plages-n-valeurs.xlsx en cliquant sur ce lien,
• Double cliquer sur le fichier téléchargé pour l'ouvrir dans Excel,
• Puis, cliquer sur le bouton Activer la modification du bandeau de sécurité,

Des valeurs numériques sont renseignées en colonne C. Leurs sommes et moyennes cycliques et alternées doivent être calculées en colonnes F et H. Pour cela, le pas du cycle renseigné en cellule F3 doit être considéré.

Opérations sur plages variables et alternées
Pour réaliser des opérations sur des plages dont la hauteur est définie dynamiquement et les poursuivre périodiquement sur les cellules du dessous, la fonction Excel Decaler est nécessaire. Au rythme de la réplication du calcul sur les lignes suivantes, elle doit être en mesure de déplacer le point de départ de la plage et d'ajuster sa hauteur dynamiquement.

• Sélectionner la première somme à calculer, soit la cellule F5,
• Taper le symbole égal (=) pour initier la formule,
• Inscrire la fonction d'addition suivie d'une parenthèse, soit : Somme(,
• Inscrire la fonction d'ajustement suivie d'une parenthèse, soit : Decaler(,
• Désigner le point de départ de la plage en cliquant sur sa cellule C4,
• Puis, enfoncer la touche F4 du clavier pour la figer, ce qui donne : $C$4,

Ce point de départ est la référence. C'est par rapport à lui, au gré de la réplication du calcul sur les lignes du dessous, que nous devrons opérer un décalage en ligne, en cohérence avec le pas souhaité par l'utilisateur, inscrit en cellule F3. Donc, nous figeons cette cellule.

• Taper un point-virgule (;) pour justement passer dans l'argument du décalage en ligne,
• Désigner le pas inscrit en cliquant sur sa cellule F3,
• Enfoncer la touche F4 du clavier pour la figer, ce qui donne : $F$3,

Lorsque ce calcul sera reproduit sur les lignes du dessous, c'est bien ce même pas qui devra être considéré. Donc sa cellule ne doit pas bouger.

• Taper le symbole de l'étoile (*) pour enclencher la multiplication,
• Ouvrir une parenthèse pour la factorisation du calcul,
• Inscrire la fonction pour l'indice de ligne suivie d'une parenthèse, soit : Ligne(,
• Désigner de nouveau la première valeur, soit la cellule C4,

Cette fois, nous ne la figeons pas. L'objectif est d'opérer le décalage en ligne en corrélation avec le pas défini, au gré de la réplication du calcul. Mais nous n'avons pas terminé sa construction.

• Fermer la parenthèse de la fonction Ligne,
• Taper le symbole moins (-) pour enclencher la soustraction,
• Inscrire de nouveau la fonction de ligne suivie d'une parenthèse, soit : Ligne(,
• Désigner une fois encore la première valeur en cliquant sur sa cellule C4,
• Cette fois, la figer à l'aide de la touche F4 du clavier, ce qui donne : $C$4,
• Fermer la parenthèse de la fonction Ligne,
• Puis, fermer la parenthèse de la factorisation,

En retranchant l'indice de ligne du point de départ figé à l'indice de ligne de la cellule qui évolue en même temps que le calcul est répliqué, nous observons un décalage qui suit le mouvement de la formule. Mais comme ce résultat est multiplié par le pas défini en cellule F3, nous déplaçons bien le point de référence sur la nouvelle plage alternée. Il reste à définir sa hauteur. Elle doit respecter ce même pas.

• Taper deux points-virgules, soit : ;;, pour ignorer l'argument du décalage en colonne,

Nous sommes ainsi directement placés dans l'argument de la hauteur à définir.

• Cliquer de nouveau sur la cellule du pas en F3,
• Enfoncer la touche F4 du clavier pour la figer, ce qui donne : $F$3,

Ce pas doit toujours être considéré par rapport à cette cellule de référence au fil de la réplication du calcul.

• Fermer la parenthèse de la fonction Decaler,
• Puis, fermer la parenthèse de la fonction Somme qui l'imbrique,
• Enfin, valider la formule par le raccourci clavier CTRL + Entrée,

Vous le savez, cette technique permet de conserver active la cellule du résultat. Ainsi, nous allons pouvoir l'exploiter dans l'enchaînement.

• Double cliquer sur la poignée de la cellule du résultat,

Ainsi, nous répliquons la logique du calcul sur les quatre lignes du dessous. Si vous modifiez la valeur du pas en cellule F3, les résultats s'actualisent aussitôt.



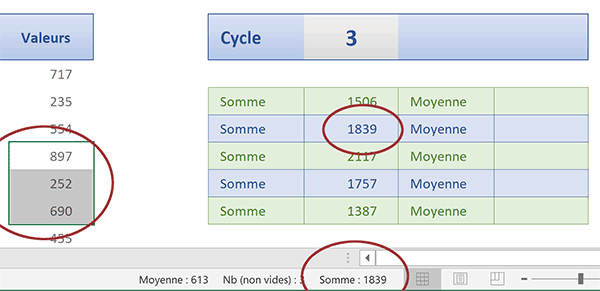
Et pour vérifier la cohérence de ce mécanisme cyclique et alterné, il n'y a rien de plus simple. Il suffit de sélectionner ensemble les valeurs de l'une des plages normalement considérées indépendamment. Dès lors, en consultant l'indication sur la somme dans la barre d'état en bas de la fenêtre Excel, vous constatez que cette donnée recoupe la synthèse du calcul pour cette même plage.

La syntaxe que nous avons construite pour la somme alternée dynamique et cyclique est la suivante :

=SOMME(DECALER($C$4; $F$3*(LIGNE(C4)-LIGNE($C$4));; $F$3))

Cette syntaxe se décline naturellement pour le calcul de la moyenne alternée en colonne H :

=MOYENNE(DECALER($C$4; $F$3*(LIGNE(C4)-LIGNE($C$4));; $F$3))

Surligner les plages alternées
Pour une solution plus évidente, nous suggérons de surligner dynamiquement les plages alternées utilisées pour les calculs cycliques des sommes et des moyennes. Ces couleurs doivent coïncider avec celles du tableau de synthèse pour un meilleur repérage. La règle de mise en forme conditionnelle doit être en mesure de déceler la borne supérieure de chaque plage alternée. Elle doit analyser les indices de chaque cellule en les ramenant à l'échelle du pas inscrit en cellule F3. Dès lors que le reste de la division de la partie entière change, nous savons que la limite de la plage est atteinte.

• Sélectionner la plage de cellules B4:C30,
• Dans la section Styles du ruban Accueil, cliquer sur le bouton Mise en forme conditionnelle,
• En bas de la liste des propositions, choisir l'option Nouvelle règle,
• Dans la boîte de dialogue qui suit, sélectionner le type : Utiliser une formule pour ...,
• Puis, cliquer dans la zone de saisie du dessous,
• Dès lors, construire la règle suivante : =MOD(ENT((LIGNE()-4)/$F$3); 2)=0,

La fonction Mod permet de calculer le reste d'une division selon le diviseur (2) fourni en second argument. A chaque fois que ce reste est nul, nous en concluons qu'il s'agit des cellules d'une même plage alternée, selon le pas inscrit en cellule F3. Pour en avoir le coeur net, nous scrutons chaque ligne de la sélection, grâce à la fonction Ligne sans argument. Nous initialisons le premier indice à zéro en retranchant 4 unités du fait des trois lignes situées au-dessus de ce tableau. Nous divisons chacun de ces indices parcourus par le pas fourni.

Prenons des exemples concrets pour bien comprendre. Le pas est défini à 5 unités. Chaque plage alternée doit donc est composée de 5 cellules en hauteur. En ligne 8, l'opération suivante est entreprise : (8-4)/5. Le résultat est 0,8. La fonction Ent ne conserve que la partie entière directement inférieure, soit 0. Donc, le reste de la division est nul et cette cellule appartient bien à la première plage. Pour la suivante en revanche, le résultat est tout autre : (9-4)/5=1. Le reste de la division n'est pas nul. La plage change pour permettre l'alternance. Et le principe s'inverse de nouveau 5 cellules plus bas. (14-4)/5=2. Le reste est bien nul. L'alternance se poursuit sur cinq cellules supplémentaires. Ces cases repérées doivent être surlignées dynamiquement.

• Cliquer sur le bouton Format en bas de la boîte de dialogue,
• Dans la boîte de dialogue qui suit, activer l'onglet Remplissage,
• Dans la palette de couleurs, choisir un vert pâle,

Il peut aussi être intéressant de régler les bordures et la police avec un vert foncé. Pour cela, il suffit d'exploiter les onglets dédiés de cette même boîte de dialogue.

• Valider ces attributs de format en cliquant sur le bouton Ok,
• De retour sur la première boîte de dialogue, valider la règle avec le bouton Ok,

Les plages apparaissent effectivement surlignées un coup sur deux et possèdent bien la hauteur définie par l'utilisateur. Et précisément, si vous modifiez cette valeur en cellule F3, les calculs comme l'alternance visuelle dynamique, s'ajustent parfaitement. Selon le même principe, il convient de repérer en bleu les plages alternées intercalées. Nous l'avons compris, avec la même syntaxe, elles sont repérées lorsque le reste de la division existe. Sur la même plage, la syntaxe de la règle à bâtir est donc la suivante : =MOD(ENT((LIGNE()-4)/$F$3); 2)=1.



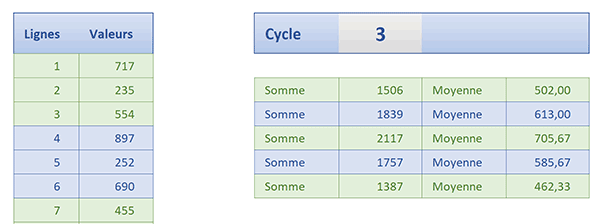
Nous avons donc abouti la solution pour réaliser des opérations sur des plages alternées de hauteurs dynamiques avec repérage visuel à l'appui.