Calculs de remboursements de prêts avec Excel

Pour partager cette vidéo sur les réseaux sociaux ou sur un site, voici son url :


Sujets que vous pourriez aussi aimer :


Simulation de remboursements d'emprunts

Dans cette formation, nous allons exploiter une fonction particulière d'Excel, pour réaliser des simulations d'emprunts. La fonction VPM d'Excel permet de calculer les mensualités ou annuités de remboursement d'un prêt, sur la base d'un taux d'intérêt et d'un montant total à emprunter.

Calcul des mensualités
Pour présenter cette fonction VPM, nous allons l'appliquer sur des valeurs prédéfinies.

• Télécharger le classeur calculs-mensualites-pret-excel.xlsx en cliquant sur son lien,
• Puis, l'ouvrir dans Excel,
• Cliquer sur l'onglet Calcul intérêts en bas de la fenêtre pour activer sa feuille,

Il s'agit d'un classeur constitué de trois feuilles. La feuille Calcul intérêts servira à présenter la fonction Excel VPM pour simuler un prêt selon un taux, un montant emprunté et une période de remboursement. Dans la feuille Simulation Emprunt, nous l'exploiterons sur une durée fixe mais en faisant varier les montants à emprunter et les taux d'intérêts, pour bien visualiser les incidences. Enfin, dans la feuille Evolution Emprunts, nous réaliserons un échéancier qui permettra de visualiser l'évolution de la part des intérêts remboursés par rapport au montant réellement remboursé.

La fonction Excel VPM requiert trois arguments. Sa syntaxe est la suivante : =-VPM(taux_interets; nombre_remboursements; valeur_empruntee). Elle renvoie par défaut une valeur négative considérant qu'il s'agit d'un versement à soustraire du montant total à rembourser. Il s'agit du calcul de la mensualité ou de l'annuité versée. On la préfixe donc du symbole moins (-) pour obtenir une valeur positive.

Nous allons commencer par calculer le montant des mensualités pour cet emprunt de 200 000 Euros, sur une période de 30 ans, soit 360 mois, avec un taux d'intérêt de 3,40%. Comme la période de remboursement est définie en mois, le taux doit être ramené au mois, donc divisé par 12.

• Sélectionner la cellule C9 et taper le symbole = pour débuter le calcul,
• Saisir ensuite le symbole moins (-),
• Taper le nom de la fonction suivi d'une parenthèse ouvrante, soit VPM(,
• Cliquer sur la cellule du taux, soit C6,
• Puis taper /12 pour ramener ce taux sur la mensualité,
• Taper un point-virgule (;) pour passer à l'argument de la période,
• Sélectionner la cellule du nombre de remboursements, soit C7,
• Taper un point-virgule (;) pour passer à l'argument du montant emprunté,
• Sélectionner la cellule de la valeur de l'emprunt, soit C5,
• Fermer la parenthèse de la formule et valider le calcul de la mensualité par Entrée,

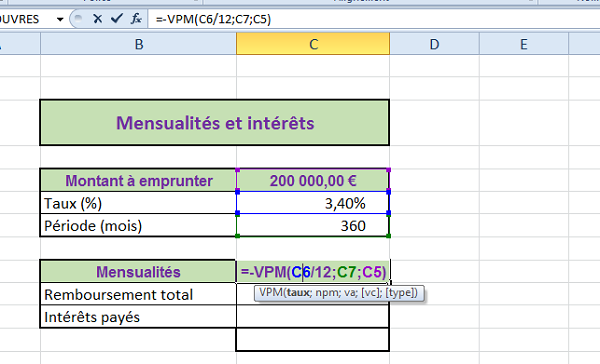
Nous obtenons le résultat de 886,96 Euros à rembourser chaque mois pendant 30 ans pour honorer l'emprunt de 200 000 Euros, tout en considérant les intérêts. Comme vous l'avez remarqué, après avoir ouvert la parenthèse de la fonction VPM, une infobulle vous guide en vous indiquant les arguments à renseigner. C'est aussi ce qu'illustre la capture ci-dessus.

Pour effectuer une simulation intéressante, nous souhaitons désormais calculer le montant total qui sera payé à l'issue, en tenant compte de ces intérêts et de la période. Il suffit donc de multiplier la mensualité par le nombre de versements.

• En cellule C10, réaliser le calcul suivant : =C9*C7,

Nous obtenons un résultat élevé, 319 306,49 Euros, semblant confirmer que plus la période de remboursement est allongée, certes la mensualité diminue, mais le montant total payé augmente. Ceci est tout à fait logique dans la mesure où les intérêts courent sur une période plus longue. Pour obtenir un résultat sans ambiguïté, il suffit de réaliser la différence entre le montant final et le montant emprunté à l'origine.

• En C11, réaliser le calcul suivant : =C10-C5,

Nous obtenons un montant de 119 306,49 Euros de plus que le montant d'origine, soit plus de la moitié à payer. Pour connaître la proportion exacte, il suffit de diviser ce montant par le montant d'origine.

• En C12, réaliser le calcul suivant : =C11/C5,

Nous obtenons le résultat de 59,7%. En d'autres termes, pour un remboursement sur 30 ans, avec un taux d'intérêts de 3,40%, il faudra payer 59,7% d'intérêts en plus du montant emprunté, fixé à 200 000 Euros. Cette somme est loin d'être anodine. Si l'on considère que le montant à emprunter est invariant, il faut donc jouer sur le taux d'intérêts et la durée de l'emprunt pour minimiser la part des intérêts.

• En C7, saisir 240 à la place de 360 et valider,

Les résultats des calculs de la simulation d'emprunt se mettent à jour instantanément. En réduisant la durée du remboursement à 20 ans, tout en conservant le même taux, la part finale des intérêts à payer tombe à 38%. Ce résultat est fort appréciable. Il implique cependant, une nette augmentation des mensualités, de plus de 250 Euros. La simulation de l'emprunt grâce à la fonction VPM confirme une évidence. Un prêt est d'autant plus intéressant que vous avez d'argent pour honorer de fortes mensualités.


Simulation d'emprunt selon le taux et le montant
Pour pousser cette analyse plus loin, le tableau de la feuille suivante, permet de réaliser une simulation de prêt, selon un taux et un montant variables. La durée de remboursement elle, reste fixe. Elle est définie en années, donc il s'agit de calculer des annuités. En conséquence, le taux ne sera pas à diviser par les 12 mois de l'année, dans le calcul de la fonction VPM.

• Cliquer sur l'onglet Simulation Emprunt en bas de la fenêtre pour activer sa feuille,

Le petit tableau en haut de la feuille, table à deux variables, propose des valeurs d'essai pour un emprunt. Seule la durée du remboursement est à considérer pour les calculs du tableau, situé plus bas.


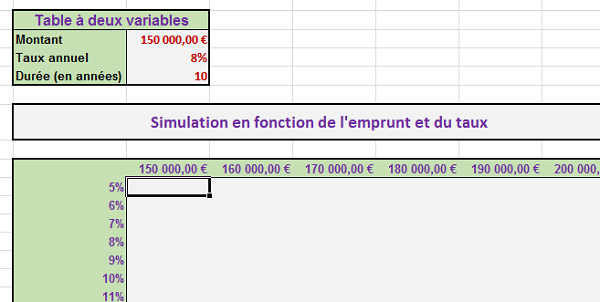
Dans ce tableau de simulation, à l'aide de la fonction Excel VPM, il s'agit donc de calculer le montant de l'annuité, en fonction du taux correspondant indiqué en colonne B et du montant correspondant à emprunter, indiqué en ligne 9.

Pour alterner les techniques, nous allons exploiter la fonction ABS sur la fonction VPM afin de rendre son résultat positif. De même, nous souhaitons réaliser un calcul qui puisse se reproduire sur l'ensemble des cellules. Nous allons donc devoir figer des cellules dans le calcul grâce aux références absolues. Et pour exploiter des techniques professionnelles, nous allons présélectionner l'ensemble de la plage avant d'initialiser le calcul, pour pouvoir le reproduire sans tirer la poignée.

• Sélectionner l'ensemble des cellules à calculer, soit C10 à H20,
• Taper le symbole = pour débuter le calcul,

Comme vous le constatez, la saisie du calcul s'effectue dans la première cellule de la plage sélectionnée. Elle est considérée comme active par défaut.

• Saisir la fonction de la valeur absolue suivi d'une parenthèse ouvrante, soit ABS(,
• Taper alors VPM(,
• Sélectionner le premier taux d'intérêt en colonne B, soit B10,
• Enfoncer trois fois de suite la touche F4 du clavier,

La touche F4 du clavier est utilisée pour figer une cellule dans un calcul en référence absolue. Des dollars encadrent alors les références de la cellule : $B$10. Dans cet exemple, le dollar devant le B indique que la cellule ne devra pas se déplacer en colonne en suivant la réplication du calcul. Le dollar devant l'indice de ligne (10), indique que la cellule ne devra pas suivre la répercussion du calcul, s'il change de ligne (Vers le bas conventionnellement). En enfonçant plusieurs fois de suite la touche F4 du clavier, nous déplaçons ces dollars. Il est justifié dans certains cas, comme ici, d'interdire une cellule de se déplacer dans une direction mais pas dans l'autre. Dans notre cas, le dollar est seulement conservé devant l'indice de colonne : $B10. C'est ce qu'illustre la capture ci-dessous.


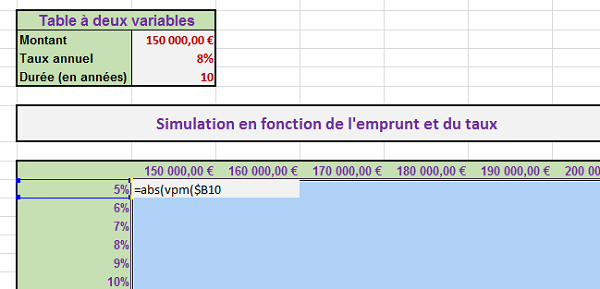
En effet, lorsque nous reproduirons le calcul vers le bas, la formule devra bien considérer les pourcentages du dessous. En revanche, lorsque nous reproduirons la formule sur les cellules situées à droite, le taux d'intérêt ne doit pas changer de colonne, car il n'existe qu'en colonne B. On fige donc la colonne. Dernière remarque avant de poursuivre le calcul, vous constatez que nous ne divisons pas le taux d'intérêt par 12 comme précédemment. En effet, il s'agit d'annuités ici :

• Taper un point-virgule (;) pour passer à l'argument du nombre de remboursements,
• Cliquer la cellule C5 de la table à deux variables, puis enfoncer la touche F4 pour la figer,

Cette fois nous conservons les deux dollars. Le nombre de remboursements est indiqué dans une cellule unique. Elle ne doit pas se déplacer avec le calcul, qu'il s'agisse de ligne ou de colonne.

• Taper un point-virgule (;) pour passer à l'argument du montant emprunté,
• Sélectionner la première cellule du montant emprunté, soit la cellule C9,
• Enfoncer deux fois la touche F4 de manière à ce que seul le dollar devant l'indice de ligne soit conservé,

En effet, cette fois lorsque le calcul sera répercuté sur les lignes du dessous, ce montant ne devra pas changer de ligne. Mais lorsque le calcul sera reproduit sur la droite, le montant devra suivre le déplacement, pour considérer les autres valeurs de la ligne. La cellule doit donc pouvoir se déplacer en colonne, c'est pourquoi il n'y a pas de dollar devant l'indice C de sa colonne.

• Fermer deux parenthèses puisque la fonction VPM est imbriquée dans la fonction ABS,
• Valider la formule par le raccourci clavier CTRL + Entrée,

Nous obtenons tous les résultats correctement calculés et répercutés sur l'ensemble des cellules du tableau, pour plusieurs raisons. Tout d'abord parce que nous avions présélectionné la plage, ensuite parce que nous avons correctement figés les références des cellules et enfin parce que nous avons ordonné la réplication par le raccourci clavier CTRL + Entrée. Comme vous l'avez remarqué, la fonction ABS d'Excel, a bien permis de retourner la valeur absolue de l'annuité calculée par la fonction VPM, soit la partie positive.


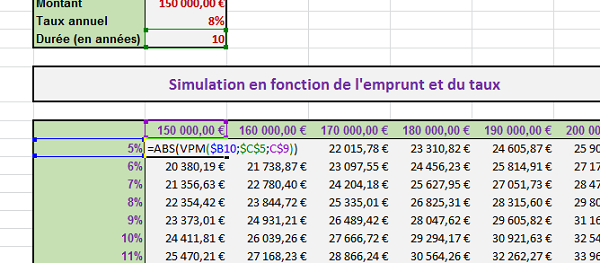
Le remboursement annuel est fort logiquement d'autant plus important que le taux d'intérêt augmente et que la valeur empruntée grandit. Si vous modifiez la valeur du nombre d'annuités en C5, vous constaterez que tous les résultats de la simulation se mettent à jour.

Echéancier de remboursement et calcul d'intérêts
Dans le dernier cas pratique, il s'agit de suivre l'évolution du remboursement d'un prêt, mois par mois. L'objectif est de constater l'évolution du remboursement des intérêts qui doit diminuer au fur et à mesure des versements, selon la mensualité calculée par la fonction VPM.

• Cliquer sur l'onglet Evolution Emprunts pour activer sa feuille,

Avant de réaliser les calculs de l'échéancier pour connaître l'évolution des intérêts remboursés et du reste dû, nous devons calculer la mensualité du remboursement de l'emprunt selon les informations du petit tableau de bord, situé sur la partie supérieure.

• Sélectionner la cellule B8 et taper le symbole = pour initialiser le calcul suivi du symbole -,
• Saisir le nom de la fonction suivi d'une parenthèse ouvrante, soit VPM(,
• Sélectionner la cellule du taux d'intérêt, soit B6,
• Saisir /12, car il s'agit d'un remboursement mensuel,
• Taper un point-virgule (;) pour passer à l'argument suivant,
• Sélectionner la cellule B7 pour désigner le nombre de remboursements,
• Taper un point-virgule (;) pour passer à l'argument suivant,
• Sélectionner enfin la cellule B5 pour désigner le montant emprunté,
• Fermer la parenthèse et valider la formule en enfonçant la touche Entrée,

L'emprunt et le taux sont relativement élevés, tandis que la période de remboursement est réduite, 60 mois soit 5 ans. Ces constats permettent de comprendre la raison pour laquelle les mensualités calculées par la fonction VPM sont si élevées. Nous obtenons en effet un résultat de 9321,51 Euros.

Pour connaître le montant des intérêts remboursés à chaque période, il s'agit de multiplier le montant total restant par le taux d'intérêt ramené au mois (divisé par 12).

• Sélectionner la cellule B11 et taper le symbole = pour débuter le calcul,
• Désigner la cellule du montant de l'emprunt, soit B5,
• Taper le symbole * du pavé numérique pour la multiplication,
• Cliquer la cellule du taux d'intérêt, soit B6,
• Taper enfin /12 pour ramener le calcul de l'intérêt sur la mensualité,
• Valider le calcul en enfonçant la touche Entrée,

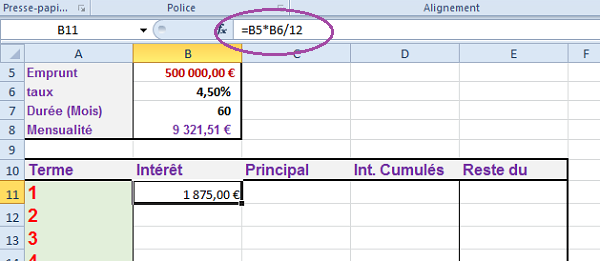
Les autres valeurs se déduisent fort logiquement de ce premier calcul. Le remboursement principal, soit le remboursement réel du prêt, est la différence entre la mensualité versée et la part des intérêts prélevée. Les intérêts cumulés pour ce premier versement sont identiques à la valeur calculée en B11. Le reste dû est la différence entre le montant à rembourser et le calcul de la part réellement remboursée (Principal). Selon ces constats :

• En C11, réaliser le calcul suivant : =B8-B11,
• En D11, saisir l'égalité suivante : =B11,
• En E11, réaliser la soustraction suivante : =B5-C11,

Maintenant que la première ligne est posée, nous allons pouvoir bâtir les calculs de la seconde ligne de manière à ce qu'ils puissent se reproduire sur l'ensemble du tableau. Comme certaines valeurs références sont issues du petit tableau de bord, nous devrons les figer. Tout d'abord en B12, il s'agit de calculer la part des intérêts remboursés pour la mensualité en cours, en fonction du reste dû et non plus de l'emprunt de départ.

• Taper le symbole = en B12 pour débuter le calcul,
• Sélectionner la cellule du reste dû, soit E11,

Nous ne figeons pas cette cellule car ses références doivent se déplacer. En effet, lorsque nous reproduirons le calcul des intérêts sur les lignes du dessous, la formule devra considérer, le reste dû suivant, situé lui aussi sur la ligne du dessous.

• Taper le symbole * pour enclencher la multiplication,
• Cliquer la cellule du taux d'intérêt, soit B6 et enfoncer la touche F4 pour la figer,

Le taux d'intérêt est en effet placé dans une cellule référence. Chaque calcul des lignes suivantes doit le désigner. Il ne doit donc pas bouger. La touche F4 du clavier encadre les références de la cellule de dollars ($B$6). Cette dernière n'a plus l'autorisation de se déplacer ni en ligne ni en colonne, dans les calculs à reproduire. Nous aurions pu nous contenter ici, de ne figer que la ligne de la cellule, en conservant seulement le dollar devant l'indice de ligne. En effet, les calculs sont à reproduire sur les lignes du dessous et non sur les colonnes d'à côté.

Le calcul du montant principal du remboursement est toujours la différence entre la valeur de la mensualité et le montant des intérêts remboursés pour la période. A l'instar du taux d'intérêt, la valeur de la mensualité est référencée dans une cellule du tableau de bord. Elle doit donc être figée pour que le calcul puisse être reproduit sur toutes les lignes du tableau.

• En cellule C12, réaliser la soustraction suivante : =$B$8-B12,

En revanche, le calcul des intérêts cumulés fait référence à des cellules dans le flux du tableau. Elles doivent donc toutes suivre le déplacement de la formule. La remarque est identique concernant le calcul du reste dû.

• En cellule D12, réaliser l'addition suivante : =D11+B12,

Il s'agit en effet de la somme des intérêts cumulés calculés précédemment avec les intérêts calculés pour la mensualité en cours.

• En cellule E12, réaliser la soustraction suivante : =E11-C12,

Il s'agit en effet d'enlever au reste dû précédemment calculé, le montant principal remboursé pour la mensualité en cours. Pour que l'échéancier soit complété, il ne reste plus qu'à reproduire l'ensemble de ces formules sur le tableau. Pour ce faire :

• Double cliquer sur la poignée de chaque cellule de calcul de cette ligne 12.

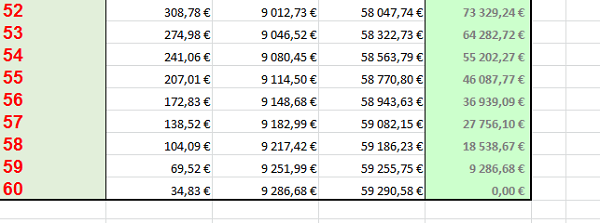
Le remboursement total du prêt est honoré à l'issue de la période de 60 mois. Ce résultat tend à confirmer la validité des calculs. Il est intéressant de constater que, plus le temps passe, plus la part des intérêts à rembourser diminue au profit de la part du remboursement principal. Cette logique est respectée puisque les intérêts sont calculés en prélevant le pourcentage du taux sur le reste dû, qui diminue chaque mois.